Uprość wyrażenie 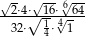 .
.
/Szkoła podstawowa
Pole prostokąta 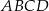 jest równe 90. Na bokach
jest równe 90. Na bokach 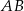 i
i 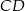 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 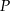 i
i 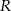 , takie, że
, takie, że 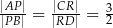 (zobacz rysunek)
(zobacz rysunek)
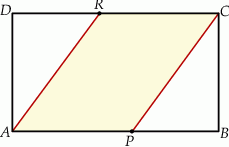
Pole czworokąta 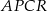 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 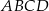 jest równe 90. Na bokach
jest równe 90. Na bokach 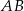 i
i 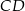 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 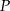 i
i 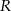 , takie, że
, takie, że 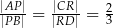 (zobacz rysunek)
(zobacz rysunek)
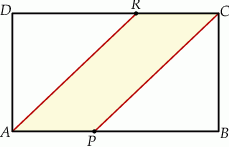
Pole czworokąta 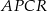 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Z punktu 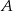 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 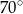 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 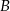 i
i 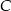 . Punkt
. Punkt 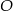 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 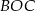 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 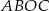 , jest równa
, jest równa
A) 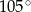 B)
B) 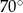 C)
C) 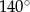 D)
D) 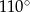
Z punktu 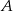 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 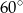 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 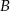 i
i 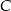 . Punkt
. Punkt 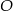 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 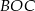 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 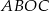 , jest równa
, jest równa
A) 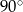 B)
B) 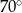 C)
C) 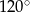 D)
D) 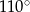
Z punktu 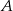 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 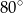 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 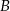 i
i 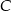 . Punkt
. Punkt 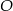 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 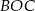 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 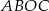 , jest równa
, jest równa
A) 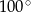 B)
B) 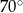 C)
C) 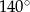 D)
D) 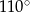
Wykres przedstawia zależność masy 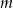 od objętości
od objętości 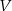 dla betonu i stali.
dla betonu i stali.
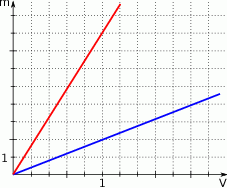
Opisz wzorem każdą z zależności. Która z zależności dotyczy betonu, a która stali?
Cena pewnego towaru wraz z 7% podatkiem VAT wynosi 69,55zł. Ile będzie kosztował ten sam towar jeżeli podatek VAT zostanie zwiększony do 22%?
Dana jest funkcja określona wzorem 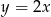 , gdzie
, gdzie  jest liczbą naturalną.
jest liczbą naturalną.
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Dla argumentu 6 funkcja przyjmuje wartość 12. | P | F |
Punkt 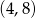 należy do wykresu tej funkcji. należy do wykresu tej funkcji. | P | F |
Dana jest funkcja określona wzorem 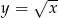 , gdzie
, gdzie  jest liczbą dodatnią.
jest liczbą dodatnią.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wartości tej funkcji są zawsze dodatnie. | P | F |
Punkt 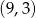 należy do wykresu tej funkcji. należy do wykresu tej funkcji. | P | F |
Dana jest funkcja określona wzorem 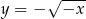 , gdzie
, gdzie  jest liczbą ujemną.
jest liczbą ujemną.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wartości tej funkcji są zawsze dodatnie. | P | F |
Punkt 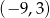 należy do wykresu tej funkcji. należy do wykresu tej funkcji. | P | F |
Wymień które liczby ze zbioru
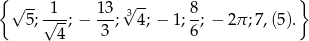
są liczbami wymiernymi.
Wymień które liczby ze zbioru
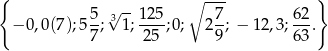
są liczbami wymiernymi.
Na rysunku przedstawiono kwadrat podzielony na 6 jednakowych prostokątów. Obwód każdego z tych prostokątów jest równy 28.

Obwód kwadratu jest równy
A) 48 B) 84 C) 96 D) 144
Organizatorzy konkursu matematycznego przygotowali zestaw, w którym było 10 pytań z algebry i 8 pytań z geometrii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z algebry.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z algebry jest równe 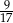 . . | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z geometrii się nie zmieniło. | P | F |
Organizatorzy konkursu z języka polskiego przygotowali zestaw, w którym było 15 pytań z gramatyki i 7 pytań z ortografii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z gramatyki.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z ortografii zwiększyło się. | P | F |
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z gramatyki jest równe 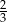 . . | P | F |
W każdej z dwóch torebek znajdują się 32 cukierki: 17 pomarańczowych, 10 jabłkowych i 5 truskawkowych. Do pierwszej torebki należy dołożyć A/B cukierki truskawkowe, aby wszystkie znajdujące się w niej cukierki truskawkowe stanowiły 25% liczby wszystkich cukierków w tej torebce.
A) 3 B) 4
Liczba cukierków pomarańczowych, które należy wyjąć z drugiej torebki, aby wśród pozostałych w niej cukierków było 40% pomarańczowych, jest C/D niż 5.
C) mniejsza D) większa
Kasia zaokrągliła liczbę 21,4456 kolejno: do jedności, do części dziesiątych, do części setnych oraz części tysięcznych. Otrzymała w ten sposób cztery liczby. O ile największa z otrzymanych liczb jest większa od najmniejszej z otrzymanych liczb?
A) 0,45 B) 0,446 C) 0,4 D) 0,5
Jeżeli Piotrek idzie bezpośrednio ze sklepu do domu, to droga zajmuje mu 15 minut. Dziś wracał jednak dłużej. Najpierw poświęcił 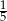 czasu na rozmowę z przyjaciółmi,
czasu na rozmowę z przyjaciółmi, 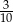 na oglądanie wystawy sklepowej, a 20 minut przyglądał się chłopcom grającym w siatkówkę. Jak długo Piotrek wracał do domu?
na oglądanie wystawy sklepowej, a 20 minut przyglądał się chłopcom grającym w siatkówkę. Jak długo Piotrek wracał do domu?
Stężenie roztworu początkowo wzrosło o 30%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 50% C) 56% D) 60%
Stężenie roztworu początkowo wzrosło o 25%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 45% B) 50% C) 55% D) 60%
Stężenie roztworu początkowo wzrosło o 20%, a po 15 minutach wzrosło o dalsze 30%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 56% C) 50% D) 60%
Cenę książki podwyższono o 20%, a następnie obniżono o 10%. Obecna cena książki stanowi 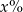 ceny początkowej. Oblicz
ceny początkowej. Oblicz  .
.
Cenę książki obniżono o 10%, a następnie podwyższono o 20%. Obecna cena książki stanowi 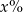 ceny początkowej. Oblicz
ceny początkowej. Oblicz  .
.
Wnuczek ma tyle miesięcy co dziadek lat. Razem mają 91 lat. Ile lat ma dziadek, a ile wnuczek?
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
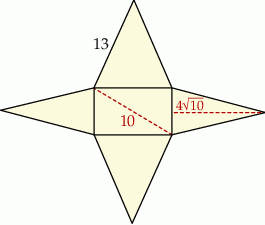
Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384
Dany jest prostokąt o bokach  i
i 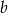 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 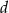 . Długość boku
. Długość boku  to 90% długości boku
to 90% długości boku  . Długość boku
. Długość boku 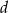 to 120% długości boku
to 120% długości boku 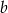 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 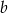 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 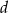 .
.
Dany jest prostokąt o bokach  i
i 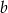 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 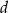 . Długość boku
. Długość boku  to 80% długości boku
to 80% długości boku  . Długość boku
. Długość boku 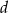 to 140% długości boku
to 140% długości boku 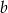 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 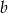 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 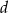 .
.
Który z zaznaczonych kątów jest kątem środkowym?

A) 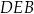 B)
B) 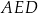 C)
C) 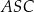 D)
D) 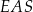
Na zlecenie klienta makler ma kupić akcje spółek 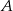 i
i 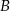 za 1000 zł. Cena jednej akcji spółki
za 1000 zł. Cena jednej akcji spółki 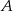 jest równa 4,25 zł, a jedna akcja spółki
jest równa 4,25 zł, a jedna akcja spółki 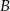 kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?
kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?
Uczniowie mieli wyznaczyć zmienną  ze wzoru
ze wzoru 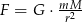 . W tabeli przedstawiono rezultaty pracy kilkorga z nich.
. W tabeli przedstawiono rezultaty pracy kilkorga z nich.
| Uczeń | Agata | Bartek | Czarek | Dorota |
| Rezultat | 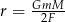 | 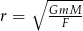 | 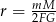 | 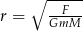 |
Kto z uczniów poprawnie wyznaczył zmienną  ?
?
A) Agata B) Bartek C) Czarek D) Dorota
Uczniowie mieli wyznaczyć zmienną 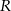 ze wzoru
ze wzoru 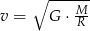 . W tabeli przedstawiono rezultaty pracy kilkorga z nich.
. W tabeli przedstawiono rezultaty pracy kilkorga z nich.
| Uczeń | Beata | Kacper | Wojtek | Ania |
| Rezultat | 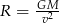 | 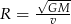 | 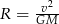 | 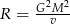 |
Kto z uczniów poprawnie wyznaczył zmienną  ?
?
A) Beata B) Kacper C) Wojtek D) Ania

