Promienie okręgów o środkach 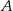 i
i 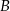 są odpowiednio równe 2018 i 995. Długość odcinka
są odpowiednio równe 2018 i 995. Długość odcinka 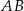 jest równa 1020.
jest równa 1020.
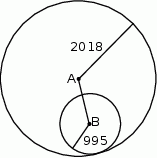
Czy okręgi te mają punkt wspólny? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | długość odcinka 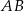 jest mniejsza od 1023. jest mniejsza od 1023. |
| B) | okręgi są styczne wewnętrznie. |
| C) | długość odcinka 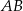 jest mniejsza od promienia większego okręgu. jest mniejsza od promienia większego okręgu. |


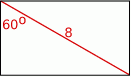

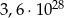 i
i 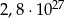 jest równa:
jest równa: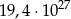
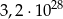
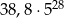
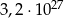
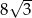
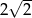
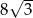
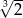
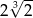
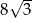
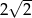
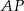 jest dwusieczną kąta
jest dwusieczną kąta 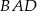 i półprosta
i półprosta 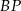 jest dwusieczną kąta
jest dwusieczną kąta 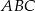 w równoległoboku
w równoległoboku 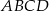 . Kąt
. Kąt 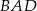 jest równy
jest równy 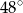 . Oblicz miarę kąta
. Oblicz miarę kąta 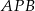 . Zapisz obliczenia.
. Zapisz obliczenia. 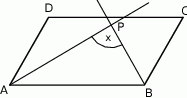
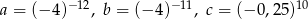 .
. 
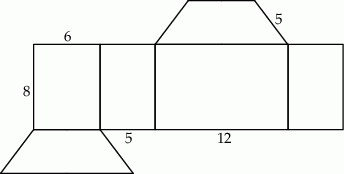
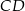 trójkąta
trójkąta 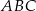 ma długość 12, bok
ma długość 12, bok 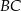 ma długość 37, a odcinek
ma długość 37, a odcinek 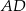 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek). 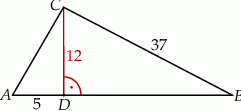
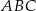 jest równe A/B.
jest równe A/B.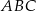 jest równy C/D.
jest równy C/D.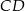 trójkąta
trójkąta 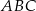 ma długość 12, bok
ma długość 12, bok 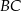 ma długość 37, a odcinek
ma długość 37, a odcinek 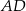 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek). 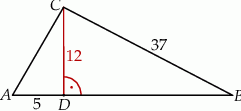
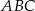 jest prostokątny.
jest prostokątny. 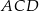 jest równa
jest równa 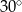 .
.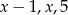 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
. 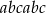 (np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową
(np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową 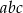 .
. 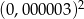 jest równa
jest równa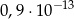
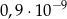
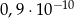
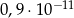
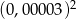 jest równa
jest równa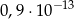
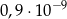
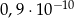
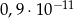
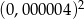 jest równa
jest równa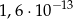
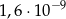
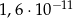
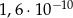
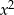 . Oblicz
. Oblicz 

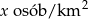 . Oblicz (w zależności od
. Oblicz (w zależności od  ) liczbę hektarów
) liczbę hektarów 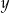 przypadającą na jednego mieszkańca tego państwa.
przypadającą na jednego mieszkańca tego państwa. 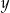 litrów benzyny, której litr kosztuje
litrów benzyny, której litr kosztuje  złotych. Wyraź
złotych. Wyraź 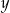 w zależności od
w zależności od  .
.  litrów benzyny na 100 km, Oblicz odległość jaką samochód może przejechać na jednym litrze benzyny.
litrów benzyny na 100 km, Oblicz odległość jaką samochód może przejechać na jednym litrze benzyny. 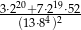 .
. 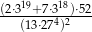 .
. 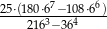 .
. 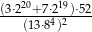 .
. 
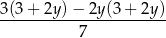
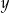 :
: