Świeże grzyby zawierają 90% wody. W wyniku suszenia masa grzybów zmniejsza się dziewięciokrotnie. Ile procent wody zawierają suszone grzyby?
/Konkursy/Zadania
Dla jakich liczb całkowitych dodatnich 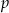 liczby
liczby 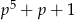 i
i 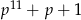 są pierwsze.
są pierwsze.
Udowodnij, że jeżeli 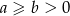 to
to 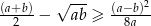 .
.
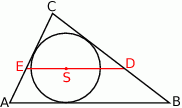
Okrąg przecina boki czworokąta 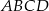 kolejno w punktach
kolejno w punktach 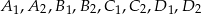 (zobacz rysunek).
(zobacz rysunek).
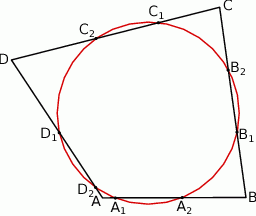
Wykaż, że jeżeli 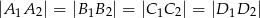 , to w czworokąt
, to w czworokąt 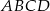 można wpisać okrąg.
można wpisać okrąg.
Wykaż, że dla dowolnych dodatnich liczb 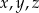 spełniona jest nierówność
spełniona jest nierówność
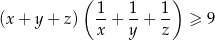
Uzasadnij, że jeżeli 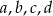 są liczbami dodatnimi to
są liczbami dodatnimi to
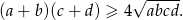
Uzasadnij, że dla dowolnych liczb naturalnych 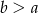 zachodzi równość
zachodzi równość 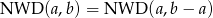 .
.
Przez środek 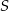 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 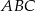 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 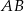 , która przecina boki
, która przecina boki 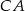 i
i 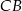 odpowiednio w punktach
odpowiednio w punktach 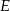 i
i 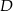 .
.
Wykaż, że 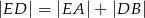 .
.
Dany jest trapez prostokątny 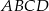 o podstawach
o podstawach 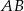 i
i 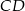 , w którym boki
, w którym boki 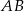 i
i 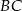 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 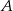 i
i 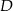 przecinają się w punkcie
przecinają się w punkcie 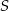 leżącym na boku
leżącym na boku 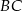 . Wykaż, że
. Wykaż, że 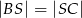 .
.
W trójkącie równoramiennym 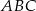 (
(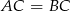 ) poprowadzono wysokości
) poprowadzono wysokości 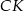 i
i 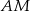 . Wiedząc że
. Wiedząc że 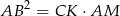 wyznacz cosinus kąta przy podstawie trójkąta.
wyznacz cosinus kąta przy podstawie trójkąta.
Świeżo skoszona trawa zawiera 60% wody, a wysuszone siano tylko 15% wody. Oblicz, ile kilogramów wysuszonego siana można otrzymać z 1 tony skoszonej trawy? Wynik podaj w zaokrągleniu do pełnych kilogramów.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 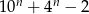 jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3.
Dany jest czworokąt wypukły 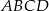 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 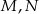 są odpowiednio środkami boków
są odpowiednio środkami boków 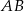 i
i 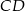 . Punkty
. Punkty 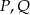 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 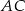 i
i 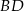 . Uzasadnij, że
. Uzasadnij, że 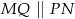 .
.
Dany jest czworokąt wypukły 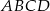 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 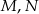 są odpowiednio środkami boków
są odpowiednio środkami boków 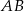 i
i 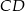 . Punkty
. Punkty 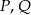 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 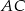 i
i 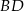 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 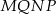 jest równoległobokiem.
jest równoległobokiem.
W prostokącie 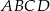 , w którym stosunek długości boków
, w którym stosunek długości boków 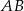 i
i 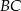 jest równy 4:3, poprowadzono dwusieczne kątów
jest równy 4:3, poprowadzono dwusieczne kątów 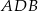 i
i 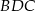 . Dwusieczne te przecinają boki
. Dwusieczne te przecinają boki 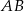 i
i 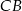 odpowiednio w punktach
odpowiednio w punktach 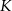 i
i 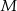 . Oblicz stosunek pola prostokąta
. Oblicz stosunek pola prostokąta 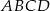 do pola trójkąta
do pola trójkąta 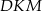 .
.
Wielokąt wypukły ma  wierzchołków,
wierzchołków, 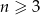 ,
, 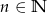 , spośród których losujemy jednocześnie dwa. Wyznacz
, spośród których losujemy jednocześnie dwa. Wyznacz  , wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od
, wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od 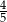 .
.
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
Długość ramienia trapezu jest równa 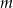 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 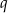 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
Punkty 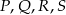 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 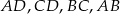 czworościanu
czworościanu 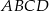 . Wykaż, że punkty
. Wykaż, że punkty 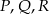 i
i 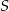 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku.
Punkt 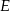 jest środkiem boku
jest środkiem boku 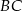 prostokąta
prostokąta 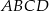 , w którym
, w którym 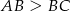 . Punkt
. Punkt 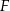 leży na boku
leży na boku 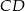 tego prostokąta oraz
tego prostokąta oraz 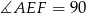 . Udowodnij, że
. Udowodnij, że 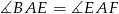 .
.
W trójkącie 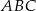 poprowadzono prostą
poprowadzono prostą 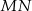 równoległą do prostej
równoległą do prostej 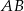 tak, że
tak, że 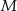 należy do
należy do 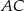 ,
, 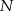 należy do
należy do 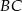 oraz
oraz 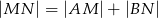 . Oblicz
. Oblicz 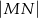 , jeśli
, jeśli 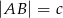 , a miary kątów trójkąta przy boku
, a miary kątów trójkąta przy boku 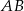 wynoszą
wynoszą  oraz
oraz 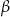 .
.

