Udowodnij, że jeżeli 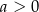 to dla wszystkich
to dla wszystkich 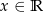 spełniona jest nierówność
spełniona jest nierówność 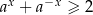 .
.
/Szkoła średnia/Nierówności
Rozwiąż nierówność 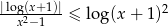 .
.
Wykaż, że dla wszystkich dodatnich liczb rzeczywistych 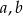 prawdziwa jest nierówność
prawdziwa jest nierówność 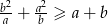 .
.
Zaznacz w układzie współrzędnych zbiór punktów 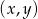 , dla których współrzędne spełniają nierówność
, dla których współrzędne spełniają nierówność 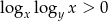 .
.
Wykaż, że dla dowolnych różnych liczb rzeczywistych 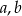 prawdziwa jest nierówność
prawdziwa jest nierówność
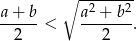
Wykaż, że jeśli 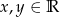 to
to 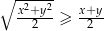 .
.
Uzasadnij, że jeżeli 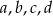 są liczbami dodatnimi to
są liczbami dodatnimi to
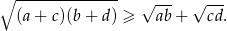
Wykaż, że dla 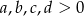 prawdziwa jest nierówność
prawdziwa jest nierówność 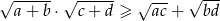 .
.
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 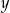 , spełniających warunek
, spełniających warunek 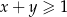 , prawdziwa jest nierówność
, prawdziwa jest nierówność
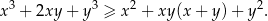
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 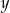 , spełniających warunek
, spełniających warunek 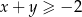 , prawdziwa jest nierówność
, prawdziwa jest nierówność
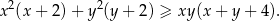
Rozwiąż nierówność 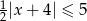 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 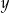 takich, że
takich, że 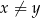 , spełniona jest nierówność
, spełniona jest nierówność
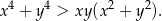
Wyznacz zbiór nieujemnych rozwiązań nierówności 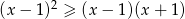 .
.
Wyznacz zbiór nieujemnych rozwiązań nierówności 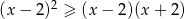 .
.
Rozwiąż nierówność 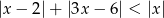 .
.
Udowodnij, że dla dowolnych liczb nieujemnych  i
i 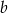 prawdziwa jest nierówność
prawdziwa jest nierówność
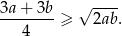
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
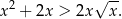
Udowodnij, że dla każdych dwóch liczb rzeczywistych 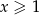 i
i 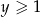 prawdziwa jest nierówność
prawdziwa jest nierówność
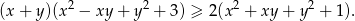
Udowodnij, że dla każdych dwóch liczb rzeczywistych 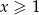 i
i 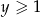 prawdziwa jest nierówność
prawdziwa jest nierówność
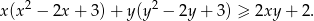
Rozwiąż nierówność 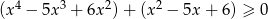 .
.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  i dla każdej liczby rzeczywistej dodatniej
i dla każdej liczby rzeczywistej dodatniej 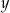 takiej, że
takiej, że 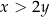 , prawdziwa jest nierówność
, prawdziwa jest nierówność
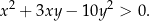
Wyznacz dopełnienie zbioru 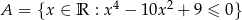 w zbiorze liczb rzeczywistych.
w zbiorze liczb rzeczywistych.
Rozwiąż nierówność 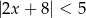 .
.
Rozwiąż nierówność 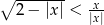 .
.
Rozwiąż graficznie nierówność 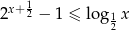 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 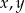 prawdziwa jest nierówność
prawdziwa jest nierówność 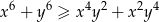 .
.

