Liczba  jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba
jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba 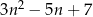 nie jest podzielna przez 4.
nie jest podzielna przez 4.
/Szkoła średnia/Liczby/Liczby całkowite/Podzielność
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 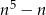 jest podzielna przez 30.
jest podzielna przez 30.
Reszta z dzielenia liczby naturalnej  przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej
przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej 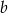 przez 6 jest równa 5. Uzasadnij, że liczba
przez 6 jest równa 5. Uzasadnij, że liczba 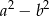 jest podzielna przez 24.
jest podzielna przez 24.
Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 16, czyli 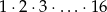 , jest podzielny przez
, jest podzielny przez 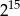 .
.
Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 21, czyli 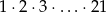 , jest podzielny przez
, jest podzielny przez 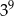 .
.
Dane są takie liczby całkowite  i
i 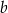 , że liczba
, że liczba 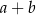 jest podzielna przez 5. Wykaż, że liczba
jest podzielna przez 5. Wykaż, że liczba 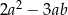 jest podzielna przez 5.
jest podzielna przez 5.
Dane są takie liczby całkowite 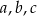 i
i 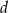 , dla których liczba
, dla których liczba 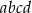 jest podzielna przez 3, ale nie jest podzielna przez 6. Wykaż, że liczba
jest podzielna przez 3, ale nie jest podzielna przez 6. Wykaż, że liczba
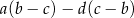
dzieli się przez 4.
Uzasadnij, że suma kwadratów trzech kolejnych liczb parzystych nigdy nie jest liczbą podzielną przez 3.
Uzasadnij, że suma kwadratów trzech kolejnych liczb nieparzystych nigdy nie jest liczbą podzielną przez 3.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 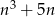 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 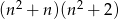 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 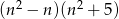 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 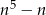 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 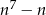 jest podzielna przez 7.
jest podzielna przez 7.

