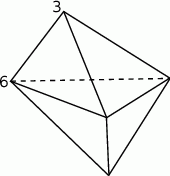
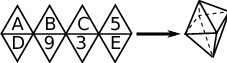
Z siatki składającej się z 8 trójkątów równobocznych można skleić ośmiościan foremny, jak na rysunku obok. Aby powstał ośmiościan magiczny, trzeba zamienić litery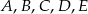 
na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe 
?
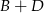A) 6 B) 7 C) 8 D) 9 E) 10
Planujemy pokolorować kratki kwadratu, używając kolorów 
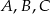i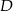 
w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).
Jakie są możliwe pokolorowania kratki zacieniowanej?
A) Tylko 
. B) Tylko 
. C) Tylko 
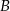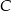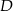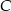. D) Albo 
, albo 
.
E) Kwadratu tego nie można tak pokolorować.
W polach szachownicy 
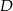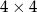chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
A) 7 B) 10 C) 14 D) 18 E) 28
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby 3 i 6 są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?
A) 9 B) 12 C) 17 D) 18 E) 24
Informacje
Zadania
Losowe zadanie