Wykaż, że jeżeli w czworokącie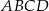 
dwusieczne kątów przy wierzchołkach 
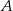i 
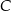przecinają dwusieczne kątów przy wierzchołkach 
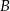i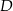 
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
/Konkursy/Zadania/Geometria/Planimetria/Czworokąt/Wpisany w okrąg
W czworokącie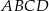 
spełniony jest warunek 
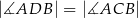. Wykaż, że na czworokącie 
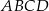można opisać okrąg.
Udowodnij, że w czworokącie wpisanym w okrąg suma iloczynów długości przeciwległych boków jest równa iloczynowi długości przekątnych (twierdzenie Ptolemeusza).
Przez każde dwa sąsiednie wierzchołki czworokąta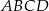 
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
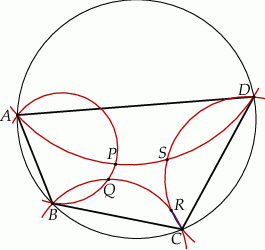
Wykaż, że punkty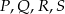 
, w których przecinają się te okręgi, leżą na jednym okręgu.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach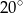 
i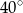 
. Oblicz miary kątów czworokąta.
