Geometryczny/Ciągi/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Ciągi/Geometryczny

Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.

Długości boków trójkąta 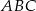ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie 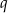. Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 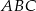ABC są równe miarom kątów trójkąta ABC .

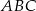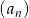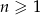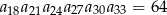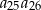Dany jest ciąg geometryczny (an) , określony dla n ≥ 1 , w którym spełniona jest równość a18a21a 24a 27a30a33 = 64 . Oblicz iloczyn a25a26 .

Wykaż, że jeżeli ciąg 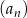(an) jest ciągiem geometrycznym, to

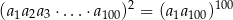
2 100 (a1a2a3 ⋅ ...⋅a100) = (a1a100)

Wykaż, że liczby 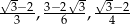√-3−2 3−-2√3 √-3−2 3 , 6 , 4 są kolejnymi wyrazami ciągu geometrycznego.

Oblicz 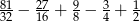81- 27- 9 3 1 32 − 16 + 8 − 4 + 2 . Wynik podaj w postaci ułamka nieskracalnego.

W ciągu geometrycznym 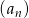(an) , określonym dla 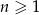n ≥ 1 , dane są: wyraz 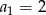a1 = 2 i suma trzech początkowych wyrazów tego ciągu 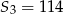S3 = 11 4 . Wiadomo ponadto, że 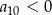a10 < 0 . Oblicz iloraz

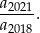
a -2021. a2018

O trapezie 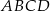ABCD wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków 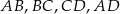AB ,BC ,CD ,AD – w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez 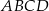ABCD jest rombem.

Wymiary prostopadłościanu o objętości 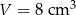3 V = 8 cm i polu powierzchni całkowitej 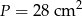P = 28 cm 2 tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.

Ukryj Podobne zadania

Długości trzech krawędzi prostopadłościanu tworzą ciąg geometryczny. Objętość bryły jest równa 27, a suma długości jej krawędzi jest równa 52. Znajdź długość najkrótszej krawędzi prostopadłościanu.

Dany jest ciąg 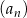(an) określony wzorem 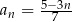5−-3n- an = 7 dla każdej liczby naturalnej 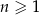n ≥ 1 . Trójwyrazowy ciąg 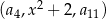(a4,x2 + 2,a11) , gdzie jest liczbą rzeczywistą, jest geometryczny. Oblicz oraz iloraz tego ciągu geometrycznego.

Ukryj Podobne zadania

Dany jest ciąg 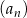(an) określony wzorem 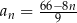66−8n an = 9 dla każdej liczby naturalnej 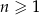n ≥ 1 . Trójwyrazowy ciąg 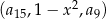(a15,1− x2,a9) , gdzie jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz oraz iloraz tego ciągu geometrycznego.

Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy.

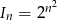Iloczyn początkowych wyrazów ciągu geometrycznego wyraża się wzorem 2 In = 2n . Oblicz pierwszy wyraz tego ciągu i jego iloraz.

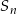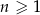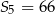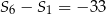W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S5 = 66 i S6 − S1 = − 33 . Wyznacz iloraz i ósmy wyraz tego ciągu.

Wyznacz wszystkie wartości 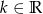k ∈ R , dla których pierwiastki wielomianu 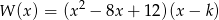W (x) = (x2 − 8x + 12)(x − k ) są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.

Iloczyn drugiego i czwartego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 9. Oblicz iloczyn pięciu początkowych kolejnych wyrazów tego ciągu.

W skończonym ciągu geometrycznym 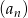(an ) wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.

Ukryj Podobne zadania

W skończonym ciągu geometrycznym 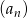(an ) wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.

Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 27, a iloczyn drugiej i trzeciej jest równy 72. Wyznacz te liczby.

Ukryj Podobne zadania

Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 52, a iloczyn drugiej i trzeciej jest równy 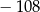− 108 . Wyznacz te liczby.

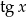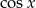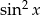Wyznacz wszystkie wartości , dla których trzy liczby: tg x , cos x , 2 sin x , tworzą ciąg geometryczny (w podanej kolejności).

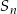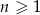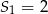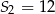W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S1 = 2 i S2 = 12 . Wyznacz iloraz i piąty wyraz tego ciągu.

Ukryj Podobne zadania

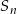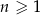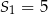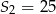W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S1 = 5 i S2 = 25 . Wyznacz iloraz i szósty wyraz tego ciągu.

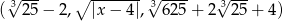Wyznacz tak, aby ciąg √3--- ∘ -------√3---- 3√ --- ( 25 − 2, |x − 4|, 6 25+ 2 25 + 4) był ciągiem geometrycznym.

Strona 2 z 7