Funkcja 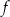 jest określona wzorem
jest określona wzorem 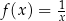 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 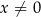 . Oblicz wartość
. Oblicz wartość 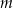 , dla której liczby
, dla której liczby 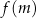 ,
, 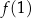 ,
, 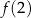 są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
/Szkoła średnia/Ciągi/Geometryczny
Uzasadnij, że ciąg określony wzorem 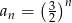 jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
Liczby 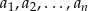 są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość
są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość 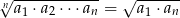 .
.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 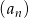 , w którym
, w którym 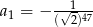 oraz
oraz 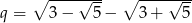 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że ich suma jest równa 10,5 oraz suma ich kwadratów jest równa 47,25.
Ciąg geometryczny 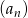 jest określony wzorem
jest określony wzorem 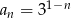 dla
dla 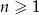 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
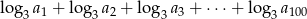 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
W trójkącie prostokątnym długości wysokości i środkowej poprowadzonej z wierzchołka kąta prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, w którym iloczyn wyrazów jest równy 8. Oblicz promień okręgu wpisanego w ten trójkąt.
Liczby dodatnie 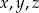 są wyrazami ciągu geometrycznego o numerach równych odpowiednio
są wyrazami ciągu geometrycznego o numerach równych odpowiednio 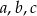 , a liczby
, a liczby 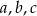 są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
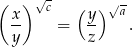
Ciąg 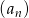 , dla
, dla 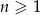 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 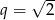 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
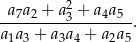
Ciąg geometryczny  ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz
ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz
Oblicz 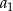 .
.
W ciągu geometrycznym 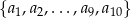 iloczyn wyrazów o numerach parzystych jest równy
iloczyn wyrazów o numerach parzystych jest równy 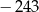 , a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
, a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
Dany jest rosnący ciąg geometryczny 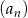 dla
dla 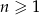 , w którym
, w którym 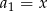 ,
, 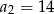 ,
, 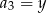 . Oblicz
. Oblicz  oraz
oraz 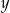 , jeżeli wiadomo, że
, jeżeli wiadomo, że 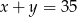 .
.
Ciąg geometryczny 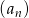 , gdzie
, gdzie 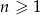 spełnia warunek
spełnia warunek 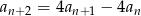 dla
dla 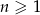 . Uzasadnij, że ciąg ten spełnia też warunek
. Uzasadnij, że ciąg ten spełnia też warunek 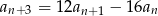 dla
dla 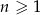 .
.
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny, w którym największy wyraz jest o 5 większy od wyrazu najmniejszego. Objętość prostopadłościanu jest równa 216. Oblicz długości krawędzi tego prostopadłościanu.
Jaką liczbą musi być  , aby liczby:
, aby liczby: 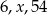 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Liczby 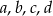 są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
Oblicz sumę 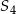 pierwszych 4 wyrazów ciągu geometrycznego
pierwszych 4 wyrazów ciągu geometrycznego 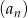 , o pierwszym wyrazie
, o pierwszym wyrazie 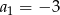 i ilorazie
i ilorazie 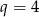 .
.
Dwudziestowyrazowy ciąg geometryczny 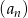 określony jest wzorem
określony jest wzorem 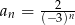 dla
dla 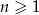 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym 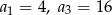 .
.
Oblicz sumę siedmiu początkowych wyrazów ciągu geometrycznego 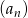 , w którym
, w którym 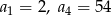 .
.
Oblicz sumę dziewięciu początkowych wyrazów rosnącego ciągu geometrycznego 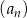 , określonego dla
, określonego dla 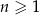 , w którym
, w którym 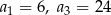 .
.
Udowodnij, że jeżeli cztery liczby dodatnie 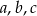 i
i 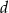 są kolejnymi wyrazami ciągu geometrycznego, to
są kolejnymi wyrazami ciągu geometrycznego, to 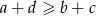 .
.

