Wszystkie wyrazy ciągu geometrycznego 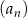 , określonego dla
, określonego dla 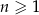 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 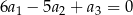 . Oblicz iloraz
. Oblicz iloraz 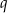 tego ciągu należący do przedziału
tego ciągu należący do przedziału 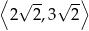 .
.
/Szkoła średnia/Ciągi/Geometryczny
Wszystkie wyrazy ciągu geometrycznego 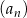 , określonego dla
, określonego dla 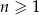 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 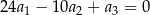 . Oblicz iloraz
. Oblicz iloraz 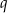 tego ciągu należący do przedziału
tego ciągu należący do przedziału 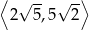 .
.
Wyrazy niezerowego ciągu geometrycznego 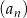 , określonego dla
, określonego dla 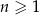 spełniają warunki:
spełniają warunki: 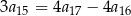 oraz
oraz 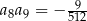 . Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.
. Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.
Wyznacz wszystkie wartości  , gdzie
, gdzie 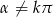 ,
, 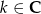 , dla których trzy liczby
, dla których trzy liczby 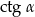 ,
, 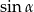 ,
, 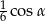 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
Dla jakich liczb 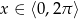 liczby
liczby 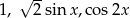 są trzema kolejnymi wyrazami ciągu geometrycznego?
są trzema kolejnymi wyrazami ciągu geometrycznego?
W ciągu geometrycznym 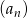 dane są iloraz
dane są iloraz 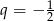 oraz suma
oraz suma
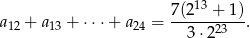
Oblicz  , dla którego ciąg
, dla którego ciąg 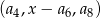 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Wyznacz liczbę  , tak aby liczby dodatnie:
, tak aby liczby dodatnie: 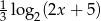 ,
, 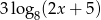 ,
, 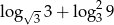 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Dane są dwa skończone ciągi geometryczne 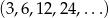 i
i 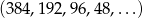 o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.
o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego wiedząc, że trzeci wyraz jest równy 18, a szósty 486.
Ciąg 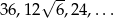 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
- Oblicz iloraz
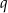 tego ciągu.
tego ciągu. - Zapisz
 -ty wyraz tego ciągu w postaci
-ty wyraz tego ciągu w postaci 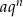
- Oblicz sumę ośmiu początkowych wyrazów tego ciągu.
W ciągu geometrycznym 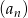 dane są iloraz
dane są iloraz 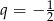 oraz suma
oraz suma
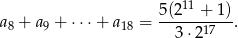
Oblicz 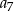 .
.
Dla jakich 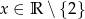 , liczby
, liczby 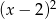 ,
, 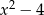 ,
, 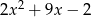 w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości
w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości  wyznacz ciąg i jego iloraz.
wyznacz ciąg i jego iloraz.
Wykaż, że dla każdej liczby naturalnej  , liczby
, liczby 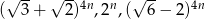 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Wyznacz wzór ogólny ciągu geometrycznego wiedząc, że 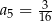 oraz
oraz 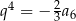 .
.
Suma ośmiu początkowych wyrazów ciągu geometrycznego 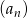 , określonego dla
, określonego dla 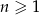 , jest równa 55760. Ponadto
, jest równa 55760. Ponadto 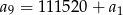 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.
Iloraz ciągu geometrycznego 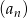 jest równy
jest równy 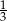 , a suma jego pięciu początkowych wyrazów wynosi
, a suma jego pięciu początkowych wyrazów wynosi 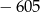 . Znajdź pierwszy wyraz ciągu
. Znajdź pierwszy wyraz ciągu 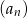 oraz określ jego monotoniczność.
oraz określ jego monotoniczność.
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
Iloczyn piątego i jedenastego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 4. Oblicz iloczyn piętnastu początkowych kolejnych wyrazów tego ciągu.
Pierwszy wyraz ciągu geometrycznego 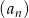 jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg
jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg 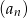 nie jest monotoniczny znajdź
nie jest monotoniczny znajdź
- jego iloraz,
- jego piąty wyraz,
- wzór na wyraz ogólny ciągu.
Dany jest ciąg geometryczny, w którym 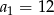 i
i 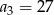 .
.
- Ile jest ciągów spełniających podane warunki? Odpowiedź uzasadnij.
- Oblicz wyraz
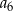 tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
Kolejne cyfry dodatniej liczby trzycyfrowej tworzą ciąg geometryczny. Suma cyfr jedności i dziesiątek jest o jeden większa od cyfry setek. Jeżeli od szukanej liczby odejmiemy liczbę złożoną z tych samych cyfr, lecz napisanych w odwrotnej kolejności to otrzymamy 495. Znajdź tę liczbę.

