Udowodnij, że w ciągu geometrycznym 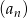 o wyrazach dodatnich iloczyn
o wyrazach dodatnich iloczyn 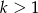 początkowych wyrazów ciągu jest równy
początkowych wyrazów ciągu jest równy 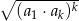 .
.
/Szkoła średnia/Ciągi/Geometryczny
Wyznacz iloraz niezerowego ciągu geometrycznego, w którym suma 10 początkowych wyrazów jest 5 razy większa od sumy pierwszych 5 wyrazów.
Wykaż, że jeżeli 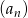 jest ciągiem geometrycznym, to ciąg
jest ciągiem geometrycznym, to ciąg 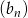 o wyrazie ogólnym określonym wzorem
o wyrazie ogólnym określonym wzorem 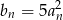 też jest ciągiem geometrycznym.
też jest ciągiem geometrycznym.
Ciąg 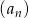 jest ciągiem geometrycznym. Wykaz, że ciąg
jest ciągiem geometrycznym. Wykaz, że ciąg 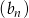 określony wzorem
określony wzorem 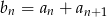 jest również ciągiem geometrycznym.
jest również ciągiem geometrycznym.
Wiadomo, że liczby 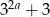 ,
, 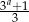 ,
, 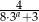 są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz
są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz  . Dla wyznaczonej wartości
. Dla wyznaczonej wartości  zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
Funkcje 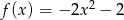 ,
, 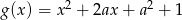 i
i 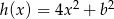 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , liczby
, liczby 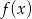 ,
,  i
i 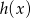 tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
Funkcje 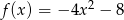 ,
, 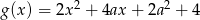 i
i 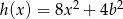 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , wartości funkcji
, wartości funkcji 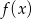 ,
, 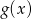 i
i 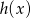 tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
Pierwszy wyraz i iloraz nieskończonego ciągu geometrycznego malejącego 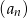 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 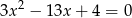 . Sprawdź czy prawdziwa jest nierówność
. Sprawdź czy prawdziwa jest nierówność 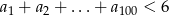 .
.
Liczby 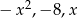 w podanej kolejności tworzą ciąg geometryczny. Oblicz
w podanej kolejności tworzą ciąg geometryczny. Oblicz  .
.
Iloczyn dziewięciu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 512. Oblicz piąty wyraz tego ciągu.
Iloczyn siedmiu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 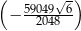 . Oblicz czwarty wyraz tego ciągu.
. Oblicz czwarty wyraz tego ciągu.
Liczby 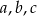 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 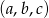 ,
, 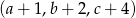 i
i 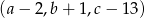 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 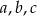 .
.
Liczby 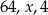 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
Oblicz sumę wszystkich liczb mniejszych od 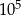 , które mogą być zapisane w postaci
, które mogą być zapisane w postaci 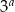 dla pewnej nieujemnej liczby całkowitej
dla pewnej nieujemnej liczby całkowitej  .
.
Oblicz 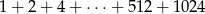 .
.
W ciągu geometrycznym 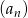 , którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.
, którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.
Wyrazy ciągu geometrycznego 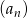 , w którym
, w którym 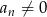 dla
dla 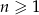 spełniają warunek
spełniają warunek
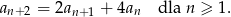
Wykaż, że wyrazy tego ciągu spełniają również warunek
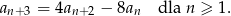
Udowodnij, że jeżeli liczby 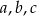 są kolejnymi wyrazami ciągu geometrycznego, to
są kolejnymi wyrazami ciągu geometrycznego, to

Iloraz ciągu geometrycznego 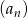 jest równy
jest równy 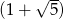 . Uzasadnij, że dla każdej liczby naturalnej
. Uzasadnij, że dla każdej liczby naturalnej 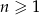 prawdziwy jest wzór
prawdziwy jest wzór 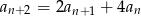 .
.
Liczby niezerowe 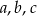 są wyrazami ciągu geometrycznego o numerach odpowiednio
są wyrazami ciągu geometrycznego o numerach odpowiednio 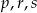 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
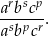
Sinus pewnego kąta ostrego  , liczba
, liczba  oraz cosinus tego samego kąta
oraz cosinus tego samego kąta  tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę
tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę 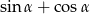 .
.
Ciąg 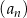 jest geometryczny o wyrazie pierwszym równym
jest geometryczny o wyrazie pierwszym równym 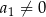 i ilorazie
i ilorazie 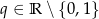 , Oblicz sumę
, Oblicz sumę 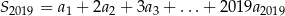 .
.
Iloraz ciągu geometrycznego 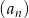 , gdzie
, gdzie 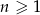 jest równy
jest równy 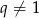 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek
, a suma 10 początkowych wyrazów tego ciągu spełnia warunek 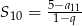 . Oblicz pierwszy wyraz tego ciągu.
. Oblicz pierwszy wyraz tego ciągu.

