Oblicz pierwszy wyraz i iloraz ciągu geometrycznego 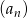 , wiedząc, że
, wiedząc, że 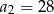 i
i 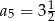 . Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
/Szkoła średnia/Ciągi/Geometryczny
Liczby 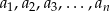 są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a
są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a  jest liczbą parzystą. Znając sumy
jest liczbą parzystą. Znając sumy
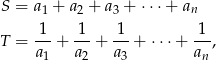
oblicz iloczyn 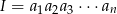 .
.
Trzynasty wyraz ciągu geometrycznego jest równy 10. Oblicz wartość iloczynu dwudziestu pięciu początkowych wyrazów tego ciągu.
Podstawy czterech logarytmów liczby  tworzą ciąg geometryczny o ilorazie
tworzą ciąg geometryczny o ilorazie  . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
. Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
Ciąg geometryczny 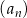 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 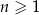 . Ilorazem tego ciągu jest liczba
. Ilorazem tego ciągu jest liczba 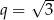 , a iloczyn 5 początkowych wyrazów tego ciągu:
, a iloczyn 5 początkowych wyrazów tego ciągu: 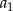 ,
, 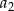 ,
, 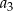 ,
, 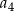 ,
, 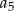 jest równy
jest równy 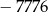 .
.
- Oblicz pierwszy wyraz tego ciągu.
- Oblicz sumę pierwszych ośmiu wyrazów tego ciągu.
Wyznacz wyraz ogólny ciągu geometrycznego 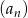 , w którym
, w którym 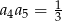 oraz
oraz 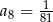 .
.
Długości boków trójkąta prostokątnego są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego. Oblicz iloraz tego ciągu.
Ciąg 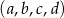 ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn
ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn 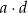 .
.
Funkcje 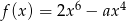 ,
, 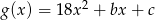 i
i 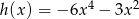 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej 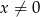 , liczby
, liczby 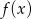 ,
, 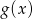 i
i 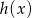 tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja
tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja 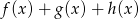 jest rosnąca na przedziale
jest rosnąca na przedziale 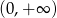 .
.
Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.
Siódmy wyraz ciągu geometrycznego 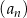 , określonego dla
, określonego dla 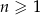 , jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz
, jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz 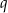 tego ciągu spełnia warunek:
tego ciągu spełnia warunek: 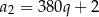 . Oblicz pierwszy wyraz oraz iloraz tego ciągu.
. Oblicz pierwszy wyraz oraz iloraz tego ciągu.
Ciąg 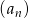 określony jest wzorem
określony jest wzorem 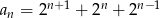 .
.
- Oblicz pierwszy i trzeci wyraz tego ciągu.
- Uzasadnij, korzystając z definicji ciągu geometrycznego, że ciąg
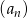 jest geometryczny.
jest geometryczny.
Wiedząc, że dla sum częściowych pewnego ciągu geometrycznego o wyrazach dodatnich prawdziwa jest równość 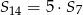 , oblicz iloraz tego ciągu.
, oblicz iloraz tego ciągu.
Niech 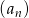 oznacza ciąg geometryczny o wyrazach dodatnich, natomiast
oznacza ciąg geometryczny o wyrazach dodatnich, natomiast 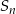 niech oznacza sumę
niech oznacza sumę  początkowych wyrazów tego ciągu. Wiedząc, że
początkowych wyrazów tego ciągu. Wiedząc, że 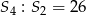 , oblicz
, oblicz 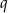 .
.
Pierwszy wyraz nieskończonego ciągu geometrycznego 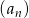 jest równy
jest równy 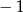 . Wyraz drugi, trzeci i czwarty spełniają warunek
. Wyraz drugi, trzeci i czwarty spełniają warunek 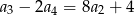 .
.
- Oblicz iloraz ciągu
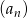 .
. - Określ, czy ciąg
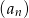 jest rosnący, czy malejący.
jest rosnący, czy malejący.
Liczby 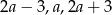 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 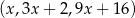 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 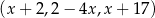 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 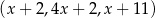 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Nieskończony ciąg geometryczny 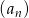 jest określony wzorem
jest określony wzorem 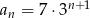 , dla
, dla 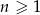 . Oblicz iloraz
. Oblicz iloraz 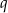 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 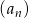 jest określony wzorem
jest określony wzorem 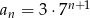 , dla
, dla 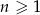 . Oblicz iloraz
. Oblicz iloraz 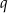 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 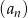 jest określony wzorem
jest określony wzorem 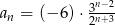 , dla
, dla 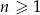 . Oblicz iloraz
. Oblicz iloraz 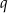 tego ciągu.
tego ciągu.
Trzy liczby dodatnie 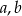 i
i  tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi
tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi 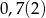 . Znajdź te liczby.
. Znajdź te liczby.
Suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 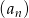 wyraża się wzorem
wyraża się wzorem 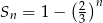 dla
dla 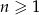 . Oblicz pierwszy wyraz ciągu i jego iloraz.
. Oblicz pierwszy wyraz ciągu i jego iloraz.
Ciąg 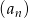 , gdzie
, gdzie 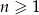 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 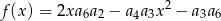 .
.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.

