Wyznacz liczbę  tak, aby liczby dodatnie
tak, aby liczby dodatnie 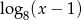 ,
, 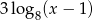 , 6 tworzyły ciąg geometryczny (w podanej kolejności).
, 6 tworzyły ciąg geometryczny (w podanej kolejności).
/Szkoła średnia/Ciągi/Geometryczny
Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli: 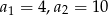 .
.
Wyznacz wszystkie ciągi geometryczne o wyrazach różnych od zera, w których każdy wyraz, rozpoczynając od wyrazu trzeciego, jest równy średniej arytmetycznej dwóch poprzednich wyrazów.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 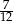 .
.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 28 oraz suma ich odwrotności jest równa 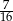 .
.
Iloraz ciągu geometrycznego 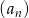 równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
- Oblicz pierwszy wyraz ciągu
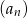 .
. - Podaj wzór na wyraz ogólny ciągu
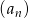 .
.
Suma 2018 początkowych wyrazów ciągu geometrycznego 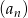 jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu
jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu 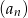 .
.
Liczby 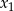 i
i 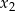 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 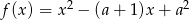 . Dla jakich
. Dla jakich 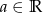 ciąg
ciąg 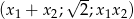 jest geometryczny?
jest geometryczny?
Wyrazy ciągu geometrycznego 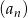 , określonego dla
, określonego dla 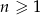 , spełniają układ równań
, spełniają układ równań
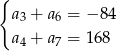
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 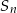 jest równa 32769.
jest równa 32769.
Wyrazy ciągu geometrycznego 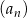 , określonego dla
, określonego dla 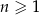 , spełniają układ równań
, spełniają układ równań
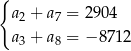
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 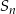 jest równa 177148.
jest równa 177148.
Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.
Liczby 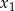 i
i 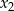 są różnymi od zera rozwiązaniami równania
są różnymi od zera rozwiązaniami równania 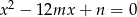 . Liczby
. Liczby 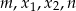 są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz
są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz 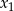 i
i 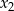 .
.
Dany jest ciąg geometryczny 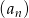 o pierwszym wyrazie równym
o pierwszym wyrazie równym 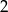 , i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych
, i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych 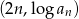 leżą na jednej prostej.
leżą na jednej prostej.
W nieskończonym ciągu geometrycznym 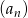 o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.
Ciąg 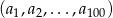 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 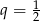 i pierwszym wyrazie równym
i pierwszym wyrazie równym 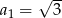 . Oblicz sumę
. Oblicz sumę
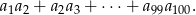
W ciągu geometrycznym 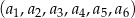 suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy
suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy 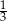 . Wyznacz wszystkie wyrazy tego ciągu.
. Wyznacz wszystkie wyrazy tego ciągu.
Dla jakich wartości  liczby
liczby 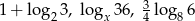 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Liczby  i
i 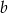 są pierwiastkami równania
są pierwiastkami równania 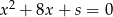 , a liczby
, a liczby  i
i 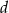 są pierwiastkami równania
są pierwiastkami równania 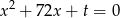 . Ciąg
. Ciąg 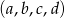 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 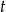 .
.
Dany jest czterowyrazowy ciąg 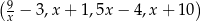 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Pierwszy wyraz niemonotonicznego ciągu geometrycznego 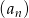 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
- Oblicz iloraz ciągu
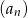 .
. - Oblicz ósmy wyraz ciągu
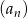 .
. - Suma kilku początkowych wyrazów ciągu
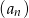 jest równa
jest równa 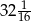 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.

