Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność
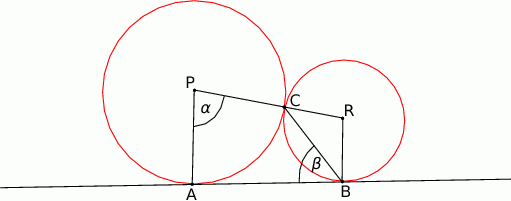
W kąt o mierze 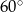 wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.
wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.
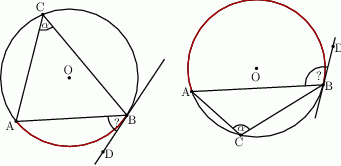
Przez punkty 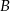 i
i 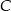 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 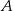 .
.
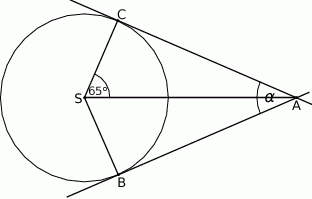
Oblicz miarę kąta 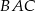 jeżeli
jeżeli 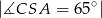 .
.
Dwa okręgi są styczne zewnętrznie, a odległość ich środków jest równa 19. Gdyby te okręgi były styczne wewnętrznie, to ta odległość wynosiłaby 5. Wyznacz długości promieni tych okręgów.
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Ramiona kąta o mierze 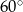 przecięto prostą
przecięto prostą 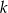 prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej
prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 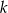 . Oblicz stosunek pól tych kół.
. Oblicz stosunek pól tych kół.
Dane są dwa okręgi o środkach w punktach 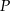 i
i 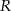 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie 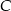 . Prosta
. Prosta 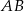 jest styczna do obu okręgów odpowiednio w punktach
jest styczna do obu okręgów odpowiednio w punktach 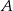 i
i 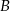 oraz
oraz 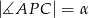 i
i 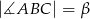 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 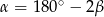 .
.
Dane są dwa okręgi o środkach w punktach 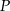 i
i 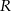 , styczne wewnętrznie w punkcie
, styczne wewnętrznie w punkcie 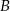 . Prosta
. Prosta 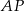 jest styczna do mniejszego okręgu w punkcie
jest styczna do mniejszego okręgu w punkcie 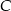 oraz
oraz 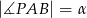 i
i 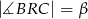 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 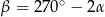 .
.
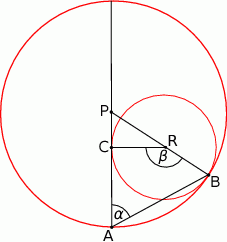
Dane są okręgi o środkach 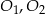 oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku
oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku 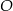 i promieniu 5. Wiadomo, że
i promieniu 5. Wiadomo, że 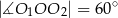 . Oblicz długość odcinka
. Oblicz długość odcinka 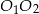 .
.
Z punktu 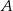 leżącego na okręgu poprowadzono średnicę
leżącego na okręgu poprowadzono średnicę 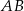 i cięciwę
i cięciwę 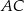 , które tworzą kąt o mierze
, które tworzą kąt o mierze 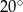 . Przez punkt
. Przez punkt 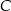 poprowadzono styczną do okręgu przecinającą prostą
poprowadzono styczną do okręgu przecinającą prostą 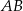 w punkcie
w punkcie 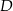 . Oblicz miary pozostałych kątów trójkąta
. Oblicz miary pozostałych kątów trójkąta 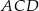 .
.
W okręgu o promieniu 5 cm poprowadzono cięciwę 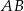 . Długość łuku
. Długość łuku 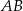 jest równa
jest równa 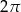 . Oblicz miarę kąta ostrego zawartego między cięciwą
. Oblicz miarę kąta ostrego zawartego między cięciwą 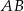 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 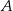 .
.
W okręgu o promieniu 8 cm poprowadzono cięciwę 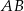 . Długość łuku
. Długość łuku 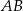 jest równa
jest równa 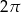 . Oblicz miarę kąta ostrego zawartego między cięciwą
. Oblicz miarę kąta ostrego zawartego między cięciwą 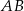 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 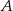 .
.
Okręgi 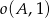 ,
, 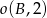 i
i 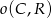 są parami styczne zewnętrznie. Oblicz
są parami styczne zewnętrznie. Oblicz 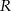 , jeśli
, jeśli 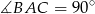 .
.
Dane są 2 koła styczne zewnętrznie o promieniach 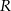 i
i  (
(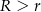 ) oraz środkach
) oraz środkach 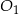 i
i 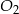 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 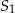 i
i 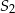 odpowiednio (
odpowiednio (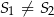 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 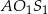 , gdzie
, gdzie 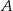 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 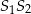 i
i 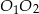 .
.
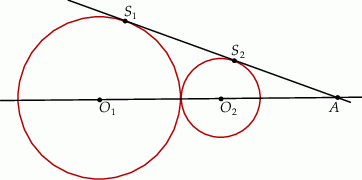
Prosta 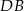 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 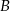 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 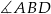 jeśli
jeśli 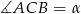 .
.
Odległość między środkami okręgów o promieniach 2 i 7 wynosi 13. Prosta 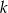 jest styczna do obu okręgów w punktach
jest styczna do obu okręgów w punktach  i
i  . Oblicz długość odcinka
. Oblicz długość odcinka 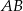 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Ramiona kąta ostrego o mierze 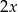 przecięto prostą
przecięto prostą 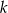 prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 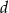 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 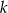 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Przez punkty 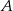 i
i 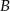 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 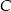 .
.
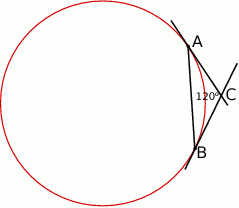
Wykaż, że jeżeli 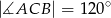 , to cięciwa
, to cięciwa 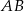 ma długość równą długości promienia okręgu.
ma długość równą długości promienia okręgu.
Do dwóch okręgów o promieniach długości 3 cm i 10 cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.
Dane są trzy okręgi o środkach 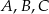 i promieniach równych odpowiednio
i promieniach równych odpowiednio 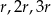 . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie
. Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 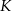 , drugi z trzecim w punkcie
, drugi z trzecim w punkcie 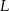 i trzeci z pierwszym w punkcie
i trzeci z pierwszym w punkcie 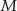 . Oblicz stosunek pola trójkąta
. Oblicz stosunek pola trójkąta 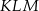 do pola trójkąta
do pola trójkąta 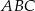 .
.

