Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 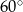 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność
Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 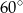 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Dwa okręgi o promieniach 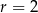 i
i 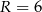 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej 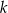 . Wykaż, że prosta
. Wykaż, że prosta 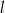 przechodząca przez środki
przechodząca przez środki 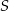 i
i 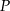 tych okręgów przecina prostą
tych okręgów przecina prostą  pod kątem
pod kątem 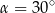 (zobacz rysunek).
(zobacz rysunek).
Z wierzchołków kwadratu o boku  , jako ze środków zakreślono 4 okręgi o promieniu
, jako ze środków zakreślono 4 okręgi o promieniu 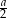 . Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
. Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
Suma pól dwóch kół stycznych zewnętrznie jest równa 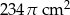 . Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.
. Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.
Każde dwa spośród trzech okręgów są zewnętrznie styczne. Oblicz promienie tych okręgów, jeśli wiadomo, że odległości między ich środkami wynoszą 8, 11, 13.
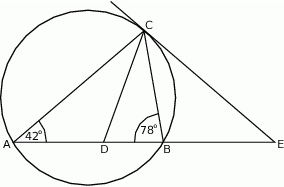
Odcinek 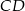 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 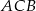 trójkąta
trójkąta 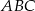 . Kąty trójkąta
. Kąty trójkąta 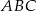 mają miary
mają miary 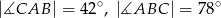 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 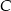 przecina prostą
przecina prostą 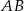 w punkcie
w punkcie 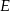 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta  .
.
Różnica promieni dwóch okręgów współśrodkowych jest równa 3. W okręgu o większym promieniu poprowadzono cięciwę styczną do drugiego okręgu. Cięciwa ta ma długość 10. Oblicz długość promieni tych okręgów.
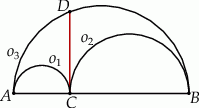
W półkole o średnicy  wpisano okrąg styczny do średnicy
wpisano okrąg styczny do średnicy 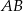 w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu
w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 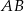 , do wpisanego okręgu oraz do średnicy
, do wpisanego okręgu oraz do średnicy 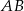 jeżeli
jeżeli 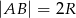 .
.
Dwa okręgi o promieniach  i
i 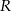 (
(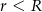 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 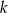 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 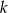 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Okręgi 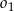 i
i 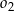 są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu
są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu 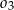 . Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa
. Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa 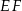 okręgu
okręgu 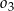 jest wspólną styczną okręgów
jest wspólną styczną okręgów 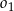 i
i 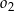 . Oblicz długość odcinka
. Oblicz długość odcinka 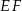 jeżeli promienie okręgów
jeżeli promienie okręgów 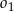 i
i 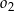 są odpowiednio równe
są odpowiednio równe 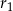 i
i 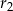 .
.
Na średnicy 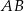 półokręgu
półokręgu 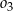 wybrano punkt
wybrano punkt 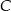 i na odcinkach
i na odcinkach 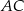 i
i 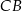 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 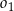 i
i 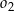 . Odcinek
. Odcinek 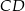 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 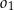 i
i 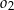 . Oblicz długość odcinka
. Oblicz długość odcinka 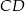 jeżeli promienie półokręgów
jeżeli promienie półokręgów 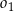 i
i 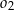 są odpowiednio równe
są odpowiednio równe 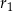 i
i 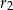 .
.
W kąt o mierze  wpisano ciąg kół w taki sposób, że pierwsze koło ma promień
wpisano ciąg kół w taki sposób, że pierwsze koło ma promień  i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
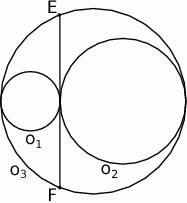
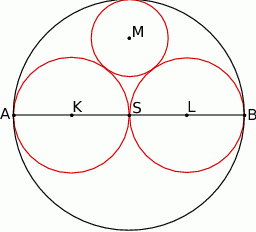
Dany jest okrąg o średnicy  i środku
i środku  oraz dwa okręgi o średnicach
oraz dwa okręgi o średnicach  i
i 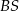 . Okrąg o środku
. Okrąg o środku 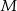 i promieniu
i promieniu  ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że
ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że 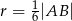 .
.
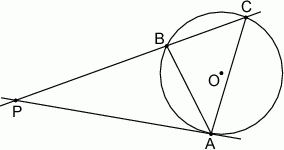
Z punktu 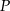 poprowadzono styczną do okręgu o środku
poprowadzono styczną do okręgu o środku 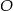 w punkcie
w punkcie 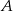 oraz sieczną, która ma z tym okręgiem dwa punkty wspólne
oraz sieczną, która ma z tym okręgiem dwa punkty wspólne 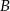 oraz
oraz 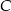 . Wiadomo, że
. Wiadomo, że 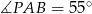 oraz
oraz 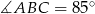 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 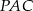 .
.
W kąt o mierze 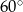 wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
Dwa styczne zewnętrznie okręgi o środkach 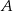 i
i 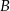 są styczne wewnętrznie do okręgu
są styczne wewnętrznie do okręgu 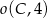 , przy czym punkty
, przy czym punkty 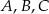 nie są współliniowe. Oblicz obwód trójkąta
nie są współliniowe. Oblicz obwód trójkąta 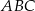 .
.
Dane dwa okręgi o środkach 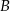 i
i 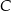 są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie
są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie 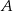 . Wiedząc, że
. Wiedząc, że 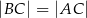 oraz promień okręgu o środku
oraz promień okręgu o środku 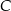 ma długość
ma długość 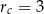 oblicz długość odcinka
oblicz długość odcinka 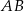 .
.
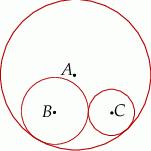
Promień okręgu wpisanego w wycinek koła o kącie środkowym 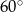 ma długość 2. Oblicz pole tego wycinka.
ma długość 2. Oblicz pole tego wycinka.
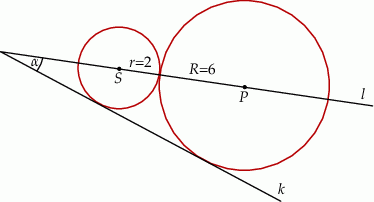
Odległości środków dwóch okręgów od wierzchołka kąta są równe 8 i 12. Okręgi te są styczne zewnętrznie i każdy z nich jest styczny do obu ramion kąta. Oblicz długości ich promieni.
Zewnętrznie styczne okręgi o środkach 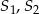 i promieniach
i promieniach 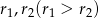 są styczne do prostej
są styczne do prostej 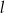 . Kąt między prostą przechodzącą przez środki okręgów i prostą
. Kąt między prostą przechodzącą przez środki okręgów i prostą 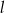 ma miarę
ma miarę 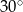 . Wyznacz długości promieni okręgów, jeśli wiadomo, że ich suma jest równa 24.
. Wyznacz długości promieni okręgów, jeśli wiadomo, że ich suma jest równa 24.
Dane są dwa okręgi zewnętrznie styczne oraz styczne wewnętrznie do trzeciego. Środki okręgów tworzą trójkąt równoramienny o bokach długości 1 i 2. Znajdź długości promieni tych okręgów (rozważ dwa przypadki).
W okrąg o promieniu 6 cm wpisano w sposób symetryczny cztery przystające okręgi. Oblicz ich promień.

