Na bokach 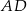 i
i 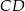 kwadratu
kwadratu 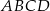 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 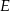 i
i 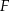 w ten sposób, że
w ten sposób, że 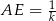 i
i 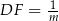 , dla
, dla 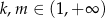 . Niech
. Niech 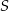 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 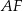 i
i 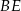
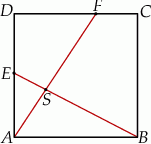
- Wykaż, że jeżeli trójkąt
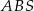 jest prostokątny to
jest prostokątny to 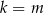 .
. - Oblicz cosinus kąta
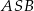 jeżeli
jeżeli 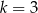 i
i 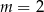 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na bokach 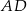 i
i 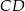 kwadratu
kwadratu 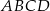 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 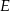 i
i 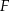 w ten sposób, że
w ten sposób, że 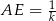 i
i 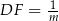 , dla
, dla 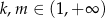 . Niech
. Niech 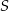 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 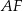 i
i 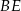

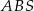 jest prostokątny to
jest prostokątny to 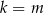 .
. 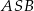 jeżeli
jeżeli 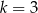 i
i 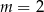 .
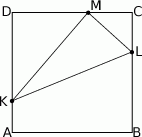
.Na bokach 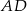 ,
, 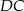 i
i 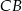 kwadratu
kwadratu 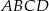 wybrano punkty
wybrano punkty 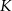 ,
, 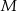 i
i 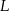 ten sposób, że
ten sposób, że 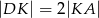 ,
, 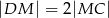 , oraz
, oraz 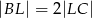 .
.
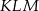 jest prostokątny.
jest prostokątny. 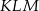 .
.
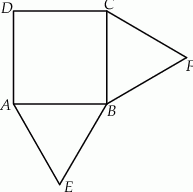
Na zewnątrz kwadratu  na bokach
na bokach  i
i 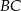 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 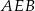 i
i 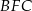 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 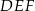 jest równoboczny.
jest równoboczny.
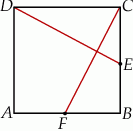
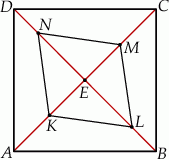
Na rysunku przedstawiono kwadrat  . Punkty
. Punkty  i
i  są środkami boków
są środkami boków 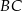 i
i 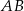 . Uzasadnij, że odcinki
. Uzasadnij, że odcinki 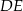 i
i 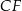 są prostopadłe.
są prostopadłe.
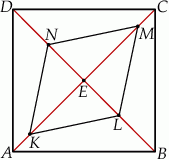
Dany jest kwadrat 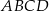 . Przekątne
. Przekątne 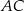 i
i 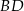 przecinają się w punkcie
przecinają się w punkcie 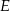 . Punkty
. Punkty 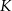 i
i 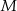 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 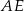 i
i 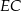 . Punkty
. Punkty 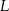 i
i 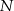 leżą na przekątnej
leżą na przekątnej 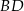 tak, że
tak, że 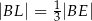 i
i 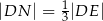 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 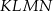 do pola kwadratu
do pola kwadratu 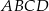 jest równy 1:3.
jest równy 1:3.
Dany jest kwadrat  . Przekątne
. Przekątne  i
i  przecinają się w punkcie
przecinają się w punkcie 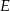 . Punkty
. Punkty 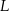 i
i 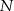 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 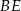 i
i 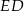 . Punkty
. Punkty 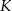 i
i 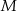 leżą na przekątnej
leżą na przekątnej 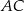 tak, że
tak, że 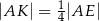 i
i 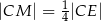 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 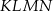 do pola kwadratu
do pola kwadratu 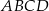 jest równy 3:8.
jest równy 3:8.
Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
Prosta przechodząca przez wierzchołek  kwadratu
kwadratu  przecina przedłużenia jego boków
przecina przedłużenia jego boków  i
i 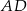 odpowiednio w punktach
odpowiednio w punktach 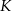 i
i 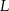 (zobacz rysunek).
(zobacz rysunek).
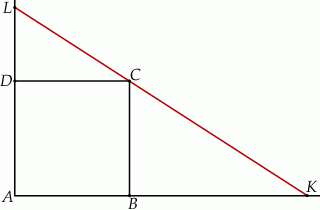
Wykaż, że
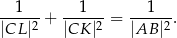
Dany jest kwadrat  o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka  zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
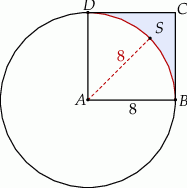
Oblicz pole powierzchni obszaru 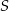 otrzymanego z kwadratu
otrzymanego z kwadratu 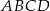 przez wycięcie części pokrytej kołem.
przez wycięcie części pokrytej kołem.
Na rysunku przedstawiono kwadrat 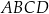 o polu 4.
o polu 4.

Punkty 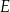 i
i 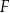 są środkami boków
są środkami boków 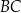 i
i 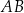 , a punkt
, a punkt 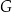 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 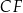 i
i 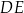 . Oblicz pole czworokąta
. Oblicz pole czworokąta 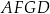
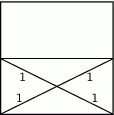
W kwadracie połączono odcinkiem środki przeciwległych boków. Wiedząc, że przekątne tak utworzonych prostokątów dzielą się na odcinki długości 1, oblicz pole wyjściowego kwadratu.
W kwadrat 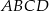 o boku długości
o boku długości 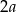 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 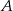 ze środkiem boku
ze środkiem boku 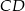 .
.
Dany jest kwadrat 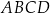 o boku długości 2. Punkt
o boku długości 2. Punkt 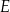 jest punktem przekątnej
jest punktem przekątnej 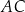 , takim że
, takim że 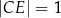 . Oblicz długość odcinka
. Oblicz długość odcinka 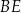 .
.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
Bok kwadratu 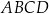 ma długość równą 12. Punkt
ma długość równą 12. Punkt 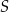 jest środkiem boku
jest środkiem boku 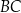 tego kwadratu. Na odcinku
tego kwadratu. Na odcinku 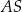 leży punkt
leży punkt 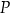 taki, że odcinek
taki, że odcinek 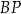 jest prostopadły do odcinka
jest prostopadły do odcinka 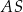 . Oblicz długość odcinka
. Oblicz długość odcinka 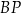 .
.
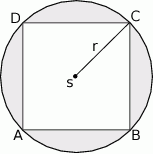
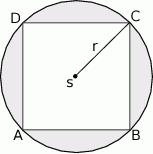
Na kwadracie 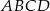 opisano okrąg o promieniu
opisano okrąg o promieniu 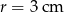 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Na kwadracie  opisano okrąg o promieniu
opisano okrąg o promieniu 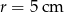 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Punkt  należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 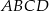 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 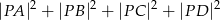 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 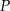 .
.
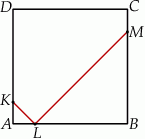
Na bokach 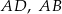 i
i 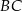 kwadratu
kwadratu 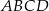 wybrano punkty
wybrano punkty 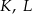 i
i 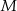 w ten sposób, że
w ten sposób, że 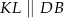 i
i 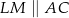 . Uzasadnij, że
. Uzasadnij, że 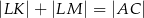 .
.
Prosta przechodząca przez środek 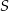 kwadratu
kwadratu 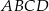 przecina proste zawierające jego boki
przecina proste zawierające jego boki 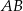 i
i 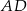 odpowiednio w punktach
odpowiednio w punktach 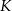 i
i 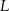 (zobacz rysunek).
(zobacz rysunek).
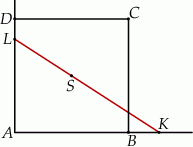
Wykaż, że
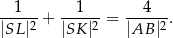
Kwadrat 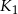 ma bok długości
ma bok długości  . Obok niego rysujemy kolejno kwadraty
. Obok niego rysujemy kolejno kwadraty 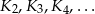 takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
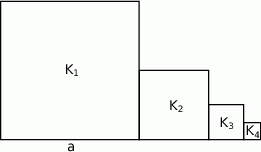
Wyznacz pole kwadratu 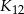 .
.
Różnica między polem koła opisanego na kwadracie a polem koła wpisanego w kwadrat jest równa 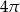 . Oblicz pole kwadratu.
. Oblicz pole kwadratu.
Oblicz pole kwadratu wiedząc, że różnica pól kół opisanego i wpisanego w ten kwadrat jest równa 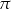 .
.
