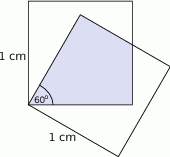
Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 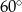 . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do
. Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 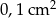 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 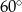 . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do
. Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 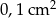 .
.

Suma długości boku kwadratu i jego przekątnej jest równa 1. Oblicz długość przekątnej kwadratu.
Przekątna kwadratu jest o 1 dłuższa od jego boku. Oblicz pole i obwód tego kwadratu.
Różnica między długością przekątnej kwadratu i długością jego boku wynosi 2 cm. Oblicz długość boku tego kwadratu.
Różnica między długością przekątnej kwadratu i długością jego boku wynosi 1 cm. Oblicz długość boku tego kwadratu.
Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 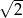 .
.
Wykaż, że stosunek długości promienia okręgu wpisanego w kwadrat do długości promienia okręgu opisanego na kwadracie jest równy 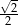 .
.
Bok 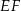 kwadratu
kwadratu 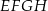 zawiera się w przekątnej
zawiera się w przekątnej 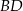 kwadratu
kwadratu 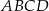 , a punkt
, a punkt 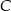 należy do odcinka
należy do odcinka 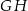 . Odcinki
. Odcinki 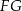 i
i 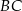 przecinają się w punkcie
przecinają się w punkcie 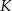 , a odcinki
, a odcinki 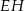 i
i 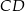 przecinają się w punkcie
przecinają się w punkcie 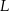 . Wykaż, że
. Wykaż, że 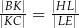 .
.
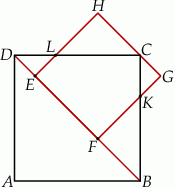
Bok 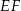 kwadratu
kwadratu 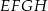 zawiera się w przekątnej
zawiera się w przekątnej 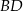 kwadratu
kwadratu 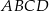 , a punkt
, a punkt 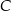 jest środkiem odcinka
jest środkiem odcinka 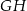 . Odcinki
. Odcinki 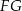 i
i 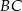 przecinają się w punkcie
przecinają się w punkcie 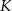 . Wykaż, że
. Wykaż, że 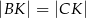 .
.
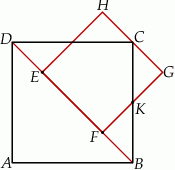
W kwadrat wpisano drugi kwadrat, którego wierzchołki leżą na bokach pierwszego i boki tworzą z bokami pierwszego kwadratu kąty o miarach 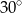 . Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
. Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 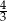 .
.
Pola dwóch kwadratów różnią się o 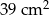 . Przekątna jednego z nich jest dłuższa o
. Przekątna jednego z nich jest dłuższa o 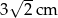 od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
W kwadrat o boku 2 wpisano drugi kwadrat w ten sposób, że bok wpisanego kwadratu tworzy z bokiem danego kąt 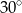 . Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
. Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
Na bokach 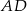 i
i 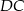 kwadratu
kwadratu 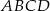 o polu 1 wybrano punkty
o polu 1 wybrano punkty 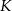 i
i 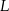 w ten sposób, że
w ten sposób, że 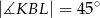 .
.
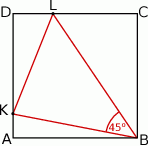
Oblicz odległość punktu 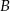 od prostej
od prostej 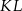 .
.
Dwa kwadraty 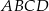 i
i 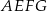 o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta
o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta 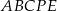 .
.
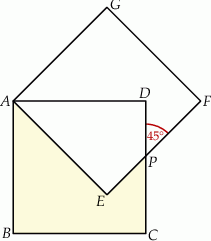
Dany jest kwadrat 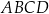 o boku długości 3. Punkty
o boku długości 3. Punkty 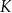 i
i 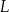 leżą na prostych – odpowiednio –
leżą na prostych – odpowiednio – 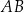 i
i 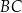 tak, że
tak, że 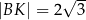 i
i 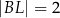 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 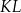 przecina przekątną
przecina przekątną 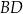 tego kwadratu w punkcie
tego kwadratu w punkcie 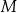 .
.
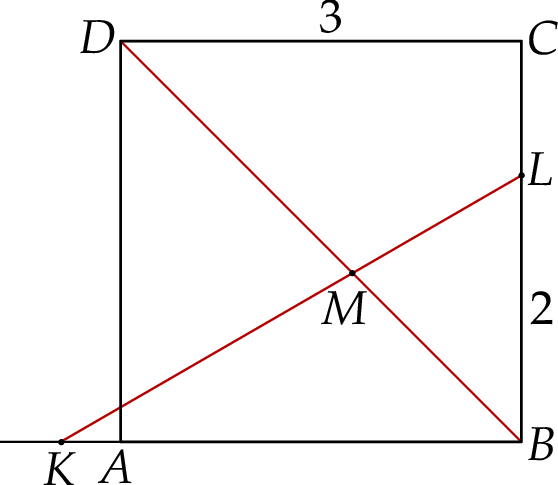
Wykaż, że 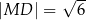 .
.
Pole kwadratu 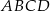 jest równe 16. Punkt
jest równe 16. Punkt 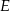 jest środkiem boku
jest środkiem boku 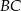 , a punkt
, a punkt 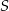 punktem przecięcia przekątnej
punktem przecięcia przekątnej 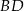 kwadratu i odcinka
kwadratu i odcinka 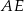 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 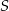 od boku
od boku 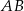 jest równa
jest równa 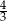 .
.
Punkt 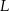 leży na boku
leży na boku 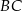 kwadratu
kwadratu 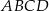 oraz
oraz 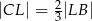 . Punkt
. Punkt 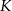 leży na przekątnej
leży na przekątnej 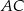 i odcinek
i odcinek 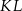 jest prostopadły do
jest prostopadły do 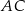 (zobacz rysunek).
(zobacz rysunek).
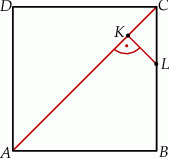
Wykaż, że 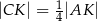 .
.
Dany jest kwadrat 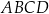 o boku długości
o boku długości  . Punkt
. Punkt 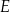 jest środkiem boku
jest środkiem boku 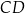 . Przekątna
. Przekątna 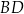 dzieli trójkąt
dzieli trójkąt 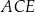 na dwie figury:
na dwie figury: 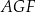 oraz
oraz 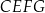 (zobacz rysunek).
(zobacz rysunek).
Oblicz pola figur 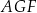 oraz
oraz 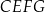 .
.
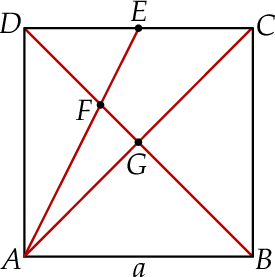
Na boku 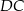 kwadratu
kwadratu 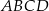 obrano punkt
obrano punkt 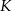 tak, że
tak, że 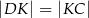 . Przekątna
. Przekątna 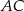 kwadratu przecina odcinek
kwadratu przecina odcinek 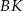 w punkcie
w punkcie 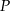 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 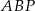 jest czterokrotnie większe niż pole trójkąta
jest czterokrotnie większe niż pole trójkąta 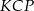 .
.
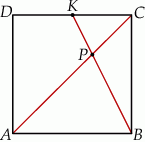
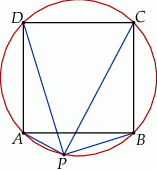
Punkt 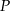 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 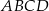 . Wykaż, że
. Wykaż, że 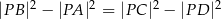 .
.
Wierzchołki kwadratu 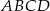 połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat
połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 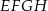 . Oblicz, jaki jest stosunek obwodów kwadratów
. Oblicz, jaki jest stosunek obwodów kwadratów 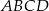 i
i 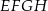 .
.
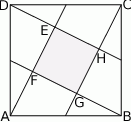
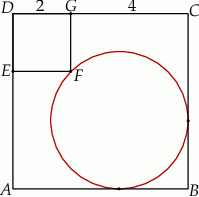
Na rysunku przedstawiono dwa kwadraty: 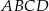 i
i 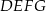 , przy czym punkty
, przy czym punkty 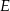 i
i 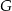 należą do odcinków
należą do odcinków 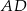 i
i 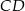 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 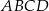 i przechodzi przez punkt
i przechodzi przez punkt 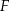 . Wykaż, że jeżeli
. Wykaż, że jeżeli 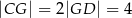 , to promień okręgu jest równy
, to promień okręgu jest równy 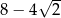 .
.
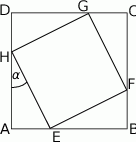
W kwadrat 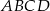 o boku długości 17 wpisano kwadrat
o boku długości 17 wpisano kwadrat 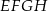 , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu
, jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 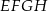 ma długość
ma długość 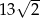 oblicz tangens kąta
oblicz tangens kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
Niech 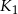 będzie kwadratem o boku długości
będzie kwadratem o boku długości  . Konstruujemy kolejno kwadraty
. Konstruujemy kolejno kwadraty 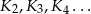 takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów
takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów 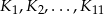 .
.
