Wykaż, że dla dowolnych dodatnich liczb 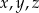 spełniona jest nierówność
spełniona jest nierówność
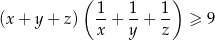
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych dodatnich liczb 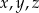 spełniona jest nierówność
spełniona jest nierówność
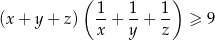
Wykaż że jeżeli 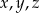 są liczbami rzeczywistymi oraz
są liczbami rzeczywistymi oraz 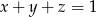 , to
, to 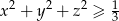 .
.
Przedstaw liczbę 20 jako sumę trzech liczb dodatnich tak, aby iloczyn tych liczb był jak największy.
Udowodnij, że dla dowolnych liczb 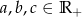 zachodzi nierówność
zachodzi nierówność
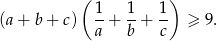
Udowodnij, że dla dowolnych liczb 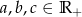 zachodzi nierówność
zachodzi nierówność
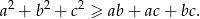
Funkcja 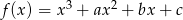 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 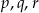 . Wykaż, że
. Wykaż, że
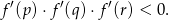
Udowodnić, że dla dowolnych nieujemnych liczb rzeczywistych 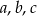 prawdziwa jest nierówność
prawdziwa jest nierówność
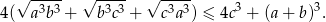
Wykaż, że jeżeli 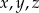 są długościami boków trójkąta to
są długościami boków trójkąta to 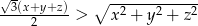 .
.
