Dany jest trapez prostokątny 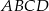 o podstawach
o podstawach 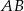 i
i 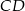 , w którym boki
, w którym boki 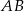 i
i 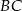 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 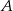 i
i 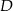 przecinają się w punkcie
przecinają się w punkcie 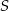 leżącym na boku
leżącym na boku 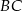 . Wykaż, że
. Wykaż, że 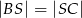 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Prostokątny
Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.
Dany jest trapez prostokątny (zobacz rysunek).
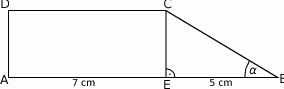
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku 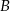 wynosi
wynosi 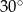 .
.
Czworokąt 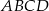 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 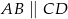 . Wykaż że
. Wykaż że
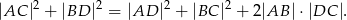
Wykaż, że w trapezie prostokątnym różnica kwadratów długości przekątnych równa jest różnicy kwadratów długości podstaw.
Podstawy trapezu prostokątnego mają długości 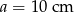 i
i 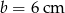 , zaś bok prostopadły do podstaw ma długość
, zaś bok prostopadły do podstaw ma długość 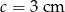 .
.
- Oblicz odległość punktu przecięcia się przekątnych tego trapezu od podstawy długości
 i ramienia długości
i ramienia długości  .
. - Czy w trapez można wpisać okrąg? Odpowiedź uzasadnij.
Podstawy trapezu prostokątnego 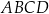 mają długości:
mają długości: 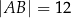 oraz
oraz 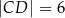 . Wysokość
. Wysokość 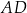 tego trapezu ma długość 24. Na odcinku
tego trapezu ma długość 24. Na odcinku 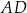 leży punkt
leży punkt 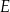 taki, że
taki, że 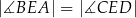 (zobacz rysunek).
(zobacz rysunek).
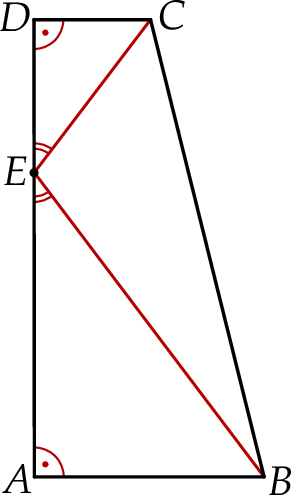
Oblicz długość odcinka 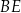 .
.
W trapezie prostokątnym 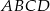 na rysunku poniżej dane są:
na rysunku poniżej dane są: 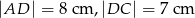 oraz
oraz 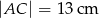 .
.
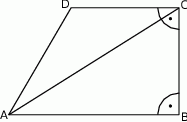
Oblicz:
- miarę kąta ostrego trapezu przy wierzchołku
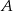 ,
, - długość odcinka łączącego środki ramion tego trapezu.
W trapezie prostokątnym 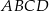 krótsze ramię
krótsze ramię 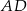 i krótsza podstawa
i krótsza podstawa 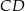 mają tę samą długość oraz
mają tę samą długość oraz 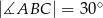 . Na podstawie
. Na podstawie 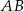 wybrano punkt
wybrano punkt 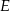 tak, że
tak, że 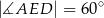 oraz
oraz 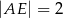 (zobacz rysunek). Oblicz długość odcinka
(zobacz rysunek). Oblicz długość odcinka 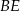 .
.
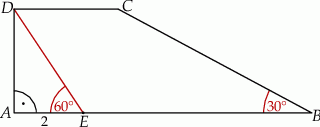
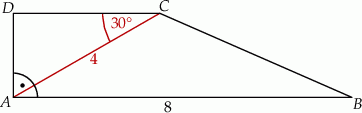
W trapezie prostokątnym 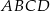 dłuższa podstawa
dłuższa podstawa 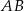 ma długość 8. Przekątna
ma długość 8. Przekątna 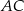 tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze 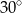 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 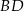 tego trapezu.
tego trapezu.
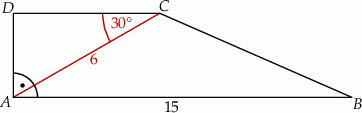
W trapezie prostokątnym 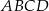 dłuższa podstawa
dłuższa podstawa 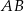 ma długość 15. Przekątna
ma długość 15. Przekątna 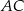 tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze 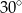 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 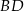 tego trapezu.
tego trapezu.
Dany jest trapez prostokątny 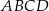 . Podstawa
. Podstawa 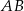 tego trapezu jest równa 26, a ramię
tego trapezu jest równa 26, a ramię 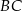 ma długość 24. Przekątna
ma długość 24. Przekątna 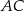 tego trapezu jest prostopadła do ramienia
tego trapezu jest prostopadła do ramienia 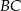 (zobacz rysunek).
(zobacz rysunek).
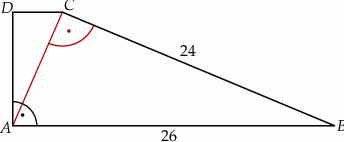
Oblicz długość ramienia 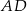 .
.
Oblicz pole i obwód trapezu prostokątnego, w którym podstawy mają długości 13 cm i 22 cm, a tangens kąta ostrego jest równy 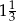 .
.
Dany jest trapez prostokątny 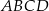 o podstawach
o podstawach 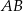 i
i 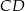 oraz wysokości
oraz wysokości 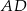 . Dwusieczna kąta
. Dwusieczna kąta 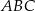 przecina ramię
przecina ramię 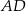 w punkcie
w punkcie 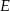 oraz dwusieczną kąta
oraz dwusieczną kąta 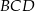 w punkcie
w punkcie 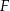 (zobacz rysunek).
(zobacz rysunek).
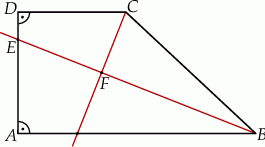
Wykaż, że w czworokącie 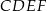 sumy miar przeciwległych kątów są sobie równe.
sumy miar przeciwległych kątów są sobie równe.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Ramiona trapezu mają długości 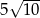 i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Podstawy trapezu prostokątnego mają długości 5 i 9 oraz cosinus kąta ostrego jest równy 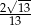 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie prostokątnym różnica długości podstaw jest równa 4,5 cm, a tangens kąta ostrego wynosi 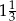 . Oblicz różnicę długości ramion tego trapezu.
. Oblicz różnicę długości ramion tego trapezu.
W trapezie prostokątnym 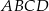 dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie
dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie 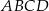 jest równy
jest równy 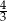 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
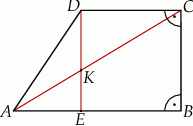
W trapezie prostokątnym 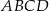 (rysunek) punkt
(rysunek) punkt 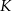 jest punktem przecięcia wysokości
jest punktem przecięcia wysokości 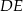 i przekątnej
i przekątnej 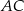 tego trapezu. Wiedząc, że
tego trapezu. Wiedząc, że 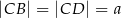 i
i 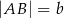 wykaż, że pole
wykaż, że pole 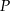 czworokąta
czworokąta 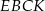 jest równe
jest równe 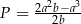 .
.
Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość 10. Oblicz długości podstaw trapezu.

