W trapezie 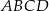 dane są długości podstaw:
dane są długości podstaw: 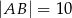 ,
, 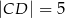 i ramion:
i ramion: 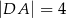 ,
, 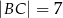 . Oblicz długość przekątnej
. Oblicz długość przekątnej 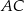 tego trapezu.
tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny
W trapezie 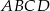 o podstawach
o podstawach 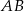 i
i 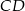 punkt
punkt 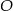 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 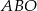 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 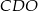 jest równe 4.
jest równe 4.
W trapezie 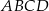 ramię
ramię 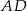 i podstawa
i podstawa 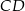 mają długość 4, a ramię
mają długość 4, a ramię 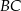 i przekątna
i przekątna 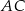 mają długość 6. Oblicz długość podstawy
mają długość 6. Oblicz długość podstawy 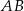 .
.
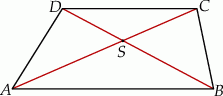
Dany jest trapez 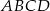 o podstawach
o podstawach 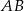 i
i 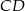 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 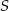 . Wykaż, że
. Wykaż, że 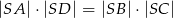 .
.
W trapezie 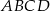 o podstawach
o podstawach 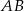 i
i 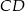 punkt
punkt 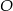 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 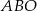 jest równe
jest równe 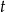 , a pole trójkąta
, a pole trójkąta 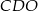 jest równe
jest równe  .
.
Punkt 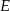 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 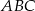 i
i 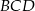 trapezu
trapezu 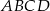 o podstawach
o podstawach 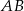 i
i 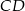 . Punkt
. Punkt 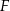 jest środkiem odcinka
jest środkiem odcinka 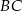 (zobacz rysunek).
(zobacz rysunek).
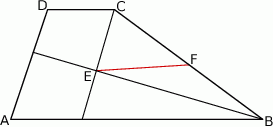
Wykaż, że 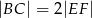 .
.
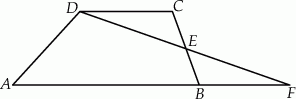
Na rysunku przedstawiono trapez 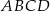 i trójkąt
i trójkąt 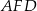 . Punkt
. Punkt 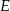 leży w połowie odcinka
leży w połowie odcinka 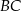 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 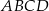 i pole trójkąta
i pole trójkąta 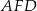 są równe.
są równe.
Oblicz pole trapezu, którego podstawy mają długości 2 i 3, a przekątne długości 3 i 4.
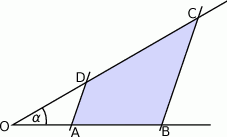
Wiedząc, że 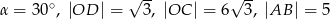 oraz
oraz 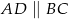 , oblicz pole i obwód trapezu
, oblicz pole i obwód trapezu  przedstawionego na rysunku.
przedstawionego na rysunku.
W trapezie 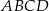 połączono środek
połączono środek 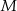 ramienia trapezu
ramienia trapezu 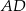 z końcami drugiego ramienia
z końcami drugiego ramienia 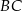 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 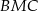 jest równe połowie pola trapezu
jest równe połowie pola trapezu 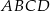 .
.
Punkt 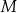 jest środkiem boku
jest środkiem boku 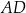 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 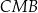 jest połową pola trapezu
jest połową pola trapezu 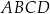 (
(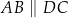 ).
).

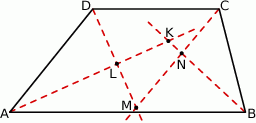
Dwusieczne kątów wewnętrznych trapezu 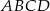 przecinają się w punktach
przecinają się w punktach 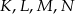 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 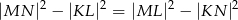 .
.
Dany jest trapez 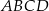 o podstawach
o podstawach 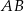 i
i 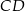 . Przekątne
. Przekątne 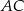 i
i 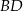 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 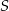 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 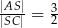 . Pole trójkąta
. Pole trójkąta 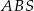 jest równe 12. Oblicz pole trójkąta
jest równe 12. Oblicz pole trójkąta 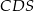 .
.
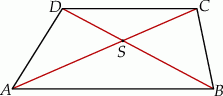
Dany jest trapez 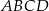 o podstawach
o podstawach 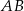 i
i 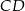 . Przekątne
. Przekątne 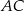 i
i 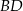 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 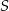 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 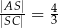 . Pole trójkąta
. Pole trójkąta 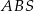 jest równe 24. Oblicz pole trójkąta
jest równe 24. Oblicz pole trójkąta 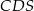 .
.
Przekątne trapezu 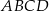 przecinają się w punkcie
przecinają się w punkcie 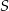 , jego podstawy mają długości
, jego podstawy mają długości 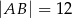 i
i 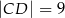 , a wysokość ma długość 8. Punkt
, a wysokość ma długość 8. Punkt 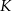 jest środkiem odcinka
jest środkiem odcinka 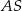 (zobacz rysunek).
(zobacz rysunek).
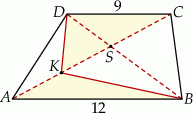
Oblicz stosunek pól trójkątów 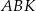 i
i 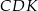 .
.
Przekątne trapezu 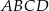 przecinają się w punkcie
przecinają się w punkcie 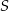 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 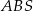 jest o 1 większy od promienia okręgu opisanego na trójkącie
jest o 1 większy od promienia okręgu opisanego na trójkącie 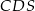 , a długości podstaw trapezu spełniają warunek
, a długości podstaw trapezu spełniają warunek 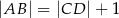 . Wykaż, że
. Wykaż, że
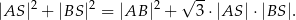
W trapezie o podstawach długości 10 cm i 6 cm oraz wysokości równej 4 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.
W trapezie o podstawach długości 12 cm i 8 cm oraz wysokości równej 6 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.
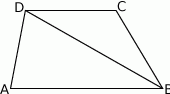
W trapezie 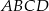 , w którym
, w którym 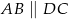 oraz
oraz 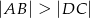 , przekątna
, przekątna 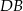 zawiera się w dwusiecznej kąta
zawiera się w dwusiecznej kąta 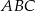 . Wykaż, że
. Wykaż, że 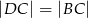 .
.
Przekątne trapezu o podstawach długości 1 i 2 są prostopadłe. Oblicz sumę kwadratów długości przekątnych trapezu.
Podstawy trapezu mają długości  i
i 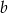 (
(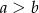 ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi
). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 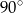 . Oblicz długość odcinka łączącego środki podstaw trapezu.
. Oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu mają długości 6 i 2, a wysokość ma długość 4. Oblicz odległość punktu przecięcia przekątnych trapezu od prostych zawierających jego podstawy.
Podstawy trapezu 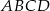 mają długości
mają długości 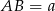 i
i 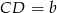 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 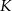 i
i 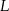 w ten sposób, że odcinek
w ten sposób, że odcinek 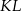 jest równoległy do podstaw oraz
jest równoległy do podstaw oraz 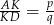 . Oblicz długość odcinka
. Oblicz długość odcinka 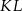 .
.

