Długość ramienia trapezu jest równa 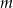 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 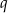 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny
Przekątne trapezu 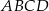 przecinają się w punkcie
przecinają się w punkcie 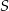 , jego podstawy mają długości
, jego podstawy mają długości 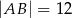 i
i 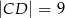 , a wysokość trapezu ma długość 8. Punkt
, a wysokość trapezu ma długość 8. Punkt 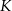 jest środkiem odcinka
jest środkiem odcinka 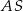 (zobacz rysunek).
(zobacz rysunek).
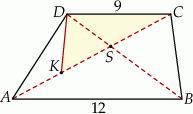
Oblicz pole trójkąta 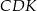 .
.
Krótsza podstawa trapezu ma długość 2, a ramiona długości 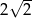 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 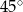 i
i 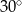 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Krótsza podstawa trapezu ma długość 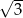 , a ramiona długości
, a ramiona długości 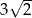 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 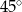 i
i 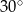 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.
Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
Wykaż, że w dowolnym trapezie suma długości ramion jest mniejsza od sumy długości przekątnych.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że pola tych trójkątów, w których jeden z boków jest ramieniem trapezu, są równe.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól trójkątów takich, że bokiem jednego jest ramię trapezu, a bokiem drugiego jest podstawa trapezu, jest równy stosunkowi długości podstaw trapezu.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól tych trójkątów, w których jeden z boków jest podstawą trapezu, jest równy stosunkowi kwadratów długości podstaw trapezu.
W trapezie 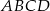 długość podstawy
długość podstawy 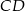 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 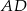 i
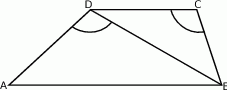
i 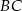 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty 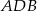 i
i 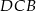 , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
Podstawy trapezu mają długości 10 i 6. Wiedząc, że suma miar kątów wewnętrznych przy dłuższej podstawie jest równa 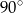 , oblicz długość odcinka łączącego środki podstaw trapezu.
, oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu 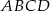 mają długości
mają długości 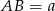 i
i 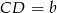 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 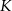 i
i 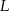 w ten sposób, że odcinek
w ten sposób, że odcinek 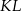 jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka
jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 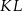 .
.
Jeżeli skrócimy wysokość trapezu o polu 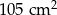 o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).
o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).
W trapezie 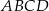 (
(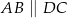 ) przekątne
) przekątne 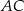 i
i 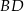 przecinają się w punkcie
przecinają się w punkcie 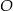 takim, że
takim, że 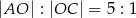 . Pole trójkąta
. Pole trójkąta 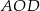 jest równe 10. Uzasadnij, że pole trapezu
jest równe 10. Uzasadnij, że pole trapezu  jest równe 72.
jest równe 72.
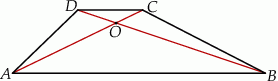
W trapezie  (
(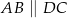 ) przekątne
) przekątne 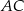 i
i 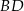 przecinają się w punkcie
przecinają się w punkcie 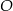 takim, że
takim, że 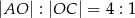 . Pole trójkąta
. Pole trójkąta 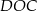 jest równe 2. Uzasadnij, że pole trapezu
jest równe 2. Uzasadnij, że pole trapezu 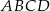 jest równe 50.
jest równe 50.
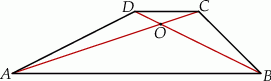
Czworokąt 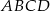 jest trapezem o podstawach
jest trapezem o podstawach 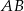 i
i 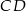 . Wykaż że
. Wykaż że
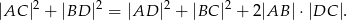
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 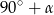 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 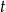 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Podstawy trapezu 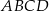 mają długości
mają długości 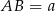 i
i 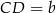 . Oblicz długość odcinka łączącego środki ramion trapezu.
. Oblicz długość odcinka łączącego środki ramion trapezu.
Proste zawierające ramiona 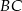 i
i 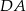 trapezu
trapezu 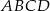 przecinają się w punkcie
przecinają się w punkcie  . Dane są:
. Dane są: 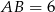 ,
, 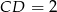 oraz obwód trójkąta
oraz obwód trójkąta 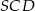 równy
równy 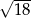 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 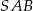 .
.
Przekątne trapezu przecinają się w punkcie 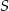 . Przez punkt
. Przez punkt 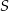 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 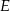 i
i 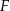 . Wykaż, że
. Wykaż, że 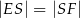 .
.
W trapezie 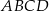 o podstawach
o podstawach 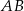 i
i 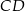 przez punkt
przez punkt 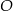 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 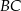 i
i 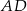 . Prosta równoległa do boku
. Prosta równoległa do boku 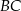 przecina bok
przecina bok 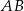 w punkcie
w punkcie 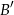 , a prosta równoległa do boku
, a prosta równoległa do boku 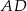 przecina bok
przecina bok 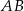 w punkcie
w punkcie 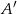 . Wykaż, że
. Wykaż, że 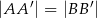 .
.
W trapezie 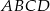 o podstawach
o podstawach 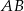 i
i 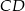 dane są długości przekątnych
dane są długości przekątnych 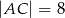 i
i 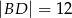 oraz pola
oraz pola 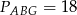 i
i 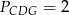 . Punkty
. Punkty 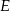 i
i 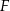 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 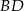 i
i  .
.
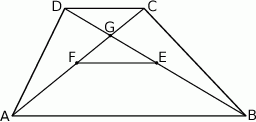
Oblicz pole trapezu 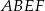 .
.
W trapezie 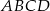 o podstawach
o podstawach 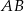 i
i 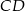 dane są długości przekątnych
dane są długości przekątnych 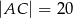 i
i 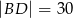 oraz pola
oraz pola 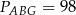 i
i 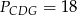 . Punkty
. Punkty 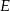 i
i 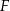 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 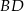 i
i 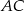 .
.
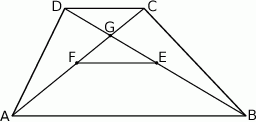
Oblicz pole trójkąta 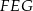 .
.
Pole trapezu jest równe 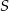 , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi 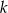 . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
W trapezie 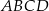 mamy
mamy 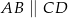 oraz
oraz 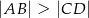 . Punkt
. Punkt 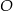 jest środkiem ramienia
jest środkiem ramienia 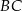 , a punkt
, a punkt 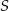 jest punktem wspólnym prostych
jest punktem wspólnym prostych 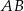
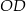 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 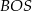 jest równe polu trójkąta
jest równe polu trójkąta 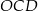 .
.
Dany jest trapez 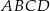 o podstawach
o podstawach 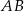 i
i 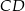 , w którym
, w którym 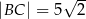 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 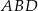 przecina prostą
przecina prostą 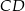 w takim punkcie
w takim punkcie 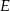 , że
, że 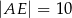 i
i 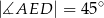 . Oblicz długość podstawy
. Oblicz długość podstawy 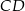 trapezu
trapezu 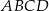 .
.
Oblicz pole trapezu 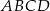 , którego podstawy mają długości
, którego podstawy mają długości 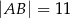 i
i 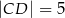 , a ramiona mają długości
, a ramiona mają długości 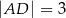 i
i 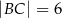 .
.

