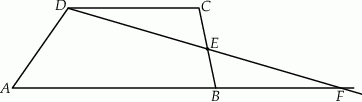
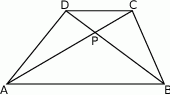
W trapezie 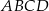 punkt
punkt 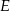 jest środkiem ramienia
jest środkiem ramienia 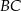 . Z wierzchołka
. Z wierzchołka 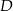 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 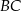 w punkcie
w punkcie 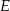 . Proste
. Proste 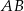 i
i 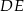 przecinają się w punkcie
przecinają się w punkcie  (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 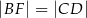 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trapezie  punkt
punkt 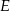 jest środkiem ramienia
jest środkiem ramienia 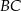 . Z wierzchołka
. Z wierzchołka 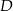 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 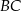 w punkcie
w punkcie 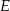 . Proste
. Proste 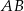 i
i 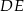 przecinają się w punkcie
przecinają się w punkcie 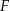 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 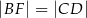 .
.

Dany jest trapez o podstawach długości  oraz
oraz 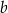 i wysokości
i wysokości 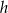 . Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość
. Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość 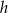 trapezu.
trapezu.
Dany jest trapez o podstawach długości  oraz
oraz 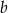 i wysokości
i wysokości 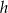 . Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość
. Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość 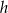 trapezu.
trapezu.
W trapezie 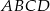 podstawa
podstawa 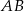 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 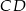 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 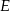 , a proste zawierające ramiona
, a proste zawierające ramiona 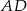 i
i 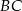 przecinają się w punkcie
przecinają się w punkcie 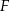 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 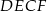 do pola trapezu
do pola trapezu 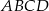 .
.
Punkt 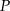 jest punktem przecięcia przekątnych trapezu
jest punktem przecięcia przekątnych trapezu 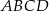 . Długość podstawy
. Długość podstawy 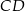 jest o 2 mniejsza od długości podstawy
jest o 2 mniejsza od długości podstawy 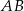 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 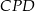 jest o 3 mniejszy od promienia okręgu opisanego na trójkącie
jest o 3 mniejszy od promienia okręgu opisanego na trójkącie 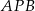 . Wykaż, że spełniony jest warunek
. Wykaż, że spełniony jest warunek 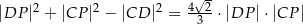 .
.
Dany jest czworokąt 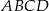 , w którym
, w którym 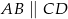 . Na boku
. Na boku 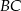 wybrano taki punkt
wybrano taki punkt 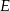 , że
, że 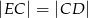 i
i 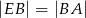 . Wykaż, że kąt
. Wykaż, że kąt 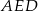 jest prosty.
jest prosty.
Prosta 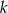 przechodząca przez punkt przecięcia przekątnych trapezu
przechodząca przez punkt przecięcia przekątnych trapezu 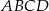 przecina jego podstawy
przecina jego podstawy 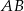 i
i 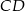 odpowiednio w punktach
odpowiednio w punktach 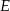 i
i 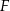 . Wykaż, że
. Wykaż, że 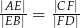 .
.
Trapez, w którym jedna z podstaw jest dwa razy dłuższa od drugiej, podzielono odcinkiem łączącym środki ramion trapezu na dwa czworokąty. Oblicz stosunek pól otrzymanych czworokątów.
Podstawy trapezu 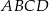 mają długości
mają długości 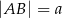 i
i 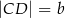 , przy czym
, przy czym 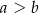 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 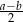 .
.
W trapezie 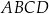 punkt
punkt 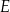 jest środkiem boku
jest środkiem boku 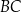 oraz
oraz 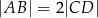 . Z wierzchołka
. Z wierzchołka 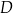 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 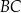 w punkcie
w punkcie 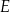 . Proste
. Proste 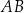 i
i 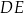 przecinają się w punkcie
przecinają się w punkcie 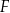 (zobacz rysunek).
(zobacz rysunek).
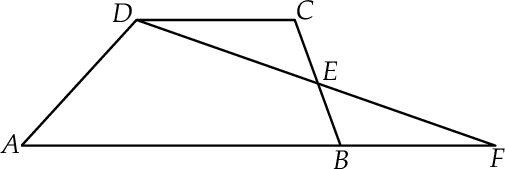
Wykaż, pole trójkąta 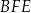 jest pięć razy mniejsze od pola czworokąta
jest pięć razy mniejsze od pola czworokąta 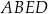 .
.
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Suma miar dwóch sąsiednich kątów trapezu jest równa 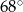 , a różnica miar dwóch pozostałych kątów jest równa
, a różnica miar dwóch pozostałych kątów jest równa 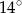 . Oblicz miary kątów tego trapezu.
. Oblicz miary kątów tego trapezu.
W trapezie 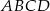 boki nierównoległe
boki nierównoległe 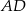 i
i 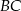 zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane
zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane 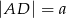 oraz
oraz 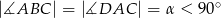 .
.
Połączono ramiona trapezu odcinkiem równoległym do podstaw i dzielącym te ramiona w stosunku 2:3 licząc od krótszej podstawy. Oblicz długość tego odcinka, jeśli wiesz, że podstawy trapezu mają długości  i
i 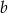 , gdzie
, gdzie 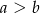 .
.
W trapezie 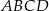 o podstawach
o podstawach 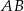 i
i 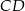 przekątne
przekątne 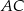 oraz
oraz 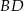 przecinają się w punkcie
przecinają się w punkcie 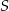 . Wykaż, że jeżeli
. Wykaż, że jeżeli 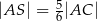 , to pole trójkąta
, to pole trójkąta 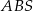 jest 25 razy większe od pola trójkąta
jest 25 razy większe od pola trójkąta 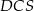 .
.
W trapezie 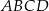 o podstawach
o podstawach 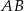 i
i 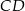 przekątne
przekątne 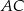 oraz
oraz 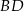 przecinają się w punkcie
przecinają się w punkcie 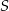 . Wykaż, że jeżeli
. Wykaż, że jeżeli 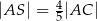 , to pole trójkąta
, to pole trójkąta 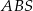 jest 16 razy większe od pola trójkąta
jest 16 razy większe od pola trójkąta 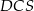 .
.
Wyprowadź wzór na pole trapezu ze wzorów na pole równoległoboku i trójkąta.
W trapezie kąty przy dłuższej podstawie to 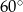 i
i 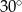 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
Podstawy trapezu mają długości 4 i 8. Kąty, jakie tworzą ramiona z dłuższą podstawą, mają miary 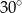 i
i 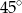 . Oblicz pole trapezu.
. Oblicz pole trapezu.
W trapezie, którego podstawy mają długości 12 cm i 6 cm, miary kątów przy dłuższej podstawie wynoszą 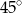 i
i 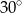 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie, którego podstawy mają długości 10 cm i 4 cm, miary kątów przy dłuższej podstawie wynoszą 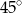 i
i 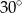 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Podstawy trapezu 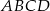 mają długości
mają długości 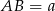 i
i 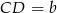 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 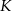 i
i 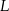 w ten sposób, że odcinek
w ten sposób, że odcinek 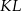 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 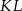 .
.
W trapezie 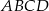 (
(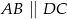 ) przekątne
) przekątne 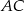 i
i 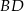 przecinają się w punkcie
przecinają się w punkcie 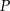 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 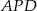 jest równe polu trójkąta
jest równe polu trójkąta 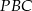 .
.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 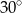 i
i 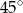 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez, w którym podstawy mają długość 6 cm i 20 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 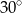 i
i 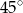 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
