Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Wpisane w kąt

Wyszukiwanie zadań

W kąt o mierze x wpisano ciąg kół w taki sposób, że pierwsze koło ma promień r i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.

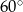W kąt o mierze ∘ 60 wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.

Promień okręgu wpisanego w wycinek koła o kącie środkowym 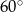∘ 60 ma długość 2. Oblicz pole tego wycinka.

Odległości środków dwóch okręgów od wierzchołka kąta są równe 8 i 12. Okręgi te są styczne zewnętrznie i każdy z nich jest styczny do obu ramion kąta. Oblicz długości ich promieni.

W kąt o mierze 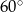∘ 60 wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.

Ramiona kąta o mierze 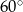∘ 60 przecięto prostą 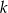k prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 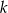k . Oblicz stosunek pól tych kół.

Ramiona kąta ostrego o mierze 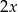2x przecięto prostą 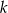k prostopadłą do dwusiecznej kąta, która jest odległa o 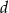d od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 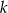k . Oblicz odległość środków tych okręgów.

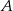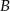Przez punkty A i B okręgu poprowadzono styczne, które przecięły się w punkcie C .

PIC

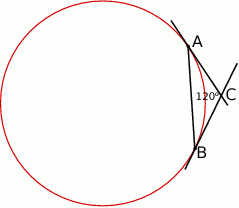
Wykaż, że jeżeli 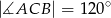|∡ACB | = 12 0∘ , to cięciwa 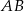AB ma długość równą długości promienia okręgu.