W trójkącie równoramiennym dane są długości podstawy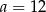 
cm i wysokości 
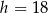cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Wpisany prostokąt
W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole prostokąta jako funkcję jego wysokości.
W trójkąt równoramienny wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie trójkąta, a dwa pozostałe są środkami ramion. Jaką część pola trójkąta stanowi pole kwadratu? Odpowiedź uzasadnij.
W trójkąt równoramienny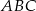 
(
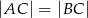) o długości podstawy 
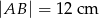wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta 
.
Ukryj
Podobne zadania
W trójkąt równoramienny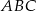 
(
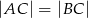) o długości podstawy 
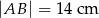wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta 
.
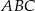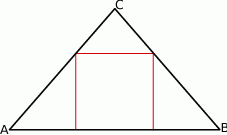
W trójkąt równoramienny o ramieniu 10 i podstawie 12 wpisano prostokąt o stosunku boków 1:4 w ten sposób, ze krótszy bok jest zawarty w podstawie trójkąta. Oblicz długości boków prostokąta.
