Dany jest czworokąt wypukły 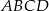 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 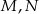 są odpowiednio środkami boków
są odpowiednio środkami boków 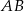 i
i 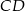 . Punkty
. Punkty 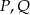 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 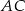 i
i 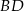 . Uzasadnij, że
. Uzasadnij, że 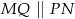 .
.
/Konkursy/Zadania/Geometria/Planimetria/Czworokąt/Różne
Dany jest czworokąt wypukły 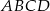 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 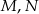 są odpowiednio środkami boków
są odpowiednio środkami boków 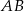 i
i 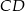 . Punkty
. Punkty 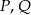 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 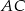 i
i 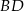 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 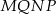 jest równoległobokiem.
jest równoległobokiem.
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
Dany jest czworokąt wypukły 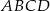 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 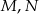 są odpowiednio środkami boków
są odpowiednio środkami boków 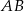 i
i 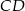 . Punkty
. Punkty 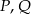 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 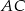 i
i 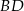 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 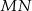 i
i 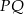 są prostopadłe, to
są prostopadłe, to 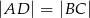 .
.
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Przekątne czworokąta wypukłego 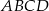 przecinają się w punkcie
przecinają się w punkcie 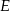 . Wiadomo, że trójkąty
. Wiadomo, że trójkąty 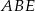 i
i 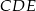 mają równe pola, długość boku
mają równe pola, długość boku 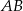 jest równa 4, a przekątna
jest równa 4, a przekątna 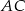 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 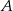 . Oblicz długość boku
. Oblicz długość boku 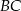 .
.

