Wyznacz przedziały monotoniczności funkcji 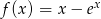 .
.
/Studia/Analiza/Funkcje
Punkt 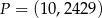 leży na paraboli o równaniu
leży na paraboli o równaniu 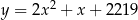 . Prosta o równaniu kierunkowym
. Prosta o równaniu kierunkowym 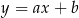 jest styczna do tej paraboli w punkcie
jest styczna do tej paraboli w punkcie 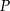 . Oblicz współczynnik
. Oblicz współczynnik 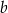 .
.
Punkt 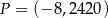 leży na paraboli o równaniu
leży na paraboli o równaniu 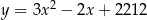 . Prosta o równaniu kierunkowym
. Prosta o równaniu kierunkowym 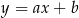 jest styczna do tej paraboli w punkcie
jest styczna do tej paraboli w punkcie 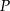 . Oblicz współczynnik
. Oblicz współczynnik 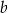 .
.
Oblicz granicę jednostronną funkcji 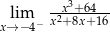 .
.
Oblicz granicę jednostronną funkcji 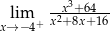 .
.
Oblicz granicę 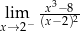 .
.
Oblicz pochodną funkcji 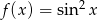 .
.
Wyznacz ekstrema funkcji 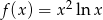 .
.
Znaleźć funkcję odwrotną do funkcji: 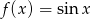 dla
dla ![π-3π- x ∈ [2; 2 ]](https://img.zadania.info/zad/4111497/HzadT1x.gif) .
.
Znaleźć funkcję odwrotną do funkcji: 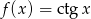 dla
dla 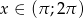 .
.
Oblicz granicę 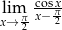 .
.
Oblicz granicę 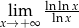 .
.
Wykaż, że wszystkie trójkąty ograniczone osiami układu współrzędnych i dowolną styczną do wykresu funkcji 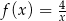 , określonej dla
, określonej dla 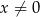 , mają równe pola.
, mają równe pola.
Funkcja 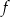 określona jest wzorem
określona jest wzorem 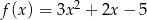 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji  , które przechodzą przez punkt
, które przechodzą przez punkt 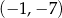 .
.
Funkcja  określona jest wzorem
określona jest wzorem 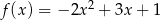 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 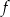 , które przechodzą przez punkt
, które przechodzą przez punkt 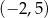 .
.
Napisz równanie stycznej do krzywej 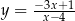 w punkcie
w punkcie 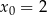 .
.
Napisz równanie stycznej do krzywej 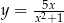 w punkcie
w punkcie 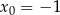 .
.
Funkcja 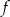 jest określona wzorem
jest określona wzorem 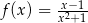 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 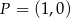 .
.
Funkcja 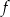 jest określona wzorem
jest określona wzorem 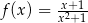 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 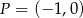 .
.
Funkcja 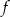 jest określona wzorem
jest określona wzorem 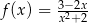 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej 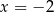 .
.
Funkcja 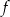 jest określona wzorem
jest określona wzorem 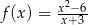 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 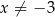 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 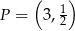 .
.
Funkcja 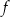 jest określona wzorem
jest określona wzorem
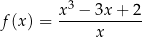
dla każdej liczby rzeczywistej  różnej od zera. W kartezjańskim układzie współrzędnych
różnej od zera. W kartezjańskim układzie współrzędnych  punkt
punkt 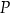 , o pierwszej współrzędnej równej 2, należy do wykresu funkcji
, o pierwszej współrzędnej równej 2, należy do wykresu funkcji 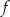 . Prosta o równaniu
. Prosta o równaniu 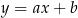 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 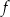 w punkcie
w punkcie 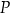 . Oblicz współczynniki
. Oblicz współczynniki  oraz
oraz 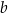 w równaniu tej stycznej.
w równaniu tej stycznej.
Funkcja 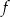 jest określona wzorem
jest określona wzorem 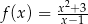 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 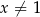 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 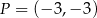 .
.
Zbadaj przebieg zmienności funkcji 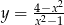 .
.
Oblicz 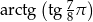 .
.
Oblicz pochodną funkcji 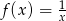 .
.
Funkcja 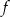 jest określona wzorem
jest określona wzorem 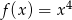 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 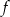 , która jest równoległa do prostej
, która jest równoległa do prostej 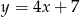 .
.
Funkcja 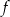 jest określona wzorem
jest określona wzorem 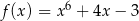 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 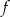 , która jest równoległa do prostej
, która jest równoległa do prostej 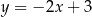 .
.
Funkcja 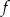 jest określona wzorem
jest określona wzorem 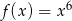 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 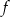 , która jest równoległa do prostej
, która jest równoległa do prostej 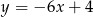 .
.
Funkcja 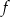 jest określona wzorem
jest określona wzorem 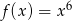 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 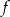 , która jest równoległa do prostej
, która jest równoległa do prostej 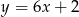 .
.
Funkcja 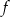 jest określona wzorem
jest określona wzorem 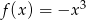 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania prostych stycznych do wykresu funkcji
. Wyznacz równania prostych stycznych do wykresu funkcji 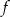 , które są równoległe do prostej
, które są równoległe do prostej 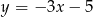 .
.
Funkcja 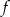 jest określona wzorem
jest określona wzorem 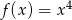 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 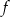 , która jest równoległa do prostej
, która jest równoległa do prostej 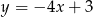 .
.
Zbadaj wypukłość funkcji 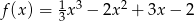 .
.
Uzasadnij, że złożenie funkcji rosnących jest funkcją rosnącą.
Uzasadnij, że złożenie funkcji rosnącej i malejącej jest funkcją malejącą.
Wyznacz przedziały monotoniczności funkcji 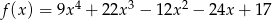 .
.
Oblicz pochodną funkcji 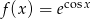 .
.
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 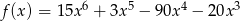 ma ekstrema lokalne.
ma ekstrema lokalne.

