Wyznacz wartość największą i najmniejszą funkcji 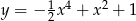 w przedziale
w przedziale 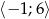 .
.
/Studia/Analiza/Funkcje
Zbadaj, na podstawie definicji, monotoniczność funkcji 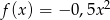 w zbiorze
w zbiorze 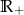 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 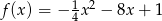 w zbiorze
w zbiorze 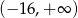 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 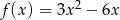 w zbiorze
w zbiorze 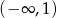 .
.
Napisz równanie stycznej do wykresu funkcji 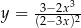 w punkcie
w punkcie 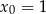 .
.
Napisz równanie stycznej do wykresu funkcji 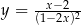 w punkcie
w punkcie 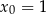 .
.
Oblicz granicę 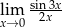 .
.
Dla jakich wartości parametru 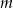 granica funkcji
granica funkcji 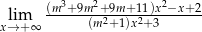 jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym
jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym 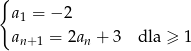
Funkcja 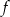 określona jest wzorem
określona jest wzorem 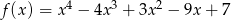 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 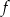 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 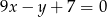 .
.
Funkcja 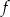 określona jest wzorem
określona jest wzorem 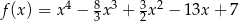 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 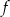 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 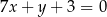 .
.
Uzasadnij, że nie istnieje granica 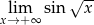 .
.
Uzasadnij, że nie istnieje granica 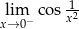 .
.
Oblicz granicę funkcji 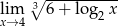 .
.
Wyznacz funkcję odwrotną do funkcji: 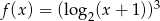 .
.
Oblicz z definicji pochodną funkcji 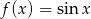 .
.
Oblicz z definicji pochodną funkcji 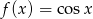 .
.
Oblicz granicę 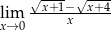 .
.
Oblicz granice jednostronne funkcji 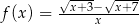 w punkcie
w punkcie 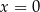 .
.
Rozważamy wszystkie proste na płaszczyźnie, które są jednocześnie styczne do wykresu funkcji homograficznej 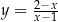 oraz do okręgu o równaniu
oraz do okręgu o równaniu 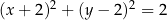 . Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
. Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
Wyznaczyć obrazy zbiorów 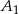 i
i 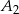 oraz przeciwobraz zbioru
oraz przeciwobraz zbioru 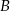 przy funkcji
przy funkcji 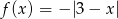 , jeżeli
, jeżeli ![A1 = [− 2,3), A 2 = (− 2,5], B = (− ∞ ,− 3]∪ {0}](https://img.zadania.info/zad/5457974/HzadT4x.gif) .
.
Wykaż, że funkcja 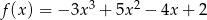 nie ma ekstremum.
nie ma ekstremum.
Oblicz pochodną funkcji 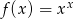 .
.
Oblicz pole trójkąta utworzonego przez prostą 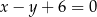 , oś
, oś 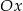 oraz styczną do wykresu funkcji
oraz styczną do wykresu funkcji 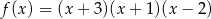 w punkcie o pierwszej współrzędnej
w punkcie o pierwszej współrzędnej 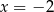 .
.
Wyznacz wszystkie proste, które są jednocześnie styczne do paraboli 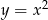 oraz okręgu o równaniu
oraz okręgu o równaniu 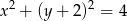 .
.
Oblicz z definicji pochodną funkcji 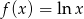 .
.
Oblicz z definicji pochodną funkcji 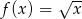 .
.
Oblicz z definicji pochodną funkcji 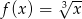 .
.
Oblicz z definicji pochodną funkcji 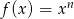 , gdzie
, gdzie 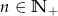 .
.

