Kwotę 240 000 podzielono na dwie części w ten sposób, że połowa różnicy tych części była równa piątej części całej kwoty. Na jakie części podzielono tę kwotę.
/Szkoła podstawowa/Zadania z treścią/Liczby
Uczeń pomyślał pewną liczbę. Następnie dodał do niej 5, otrzymaną sumę podzielił przez 3, a otrzymany iloraz pomnożył przez 4. Potem od ostatniego wyniku odjął 6. Gdy tę różnicę podzielił przez 7, to otrzymał liczbę 2. Jaką liczbę pomyślał uczeń?
Kod dostępu do komputera Andrzeja złożony jest z czterech kolejnych wielokrotności liczby 7 ustawionych od najmniejszej do największej. Suma tych wielokrotności wynosi 294. Znajdź liczby, z których złożony jest ten kod. Zapisz swoje rozumowanie.
Suma trzech liczb jest równa 2520. Jakie to liczby jeżeli ich stosunek jest równy 4:5:9?
Dane są dwie liczby dodatnie 
i 
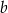, których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia: 
.
Ukryj
Podobne zadania
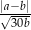Dane są dwie liczby dodatnie 
i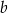 
, których stosunek wynosi 3:5. Jeżeli mniejszą z tych liczb zwiększymy o 18, a większą zmniejszymy o 55%, to stosunek otrzymanych liczb wyniesie 8:5. Oblicz wartość wyrażenia: 
.
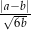Wykaż, że dla dowolnej liczby całkowitej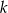 
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 
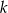jest równa -2.
