Geometria/Szkoła podstawowa - zadania z matematyki

/Szkoła podstawowa/Geometria

Oblicz pole i obwód równoległoboku przedstawionego na rysunku.

Ukryj Podobne zadania

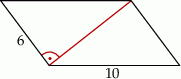
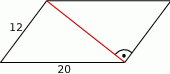
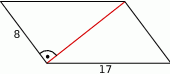
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.

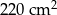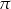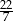Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej ﬁgury ma długość 44 cm, a jej pole jest równe 22 0 cm 2 . Oblicz objętość tego pudełka. Przyjmij przybliżenie równe 272 . Zapisz obliczenia.

Ukryj Podobne zadania

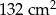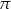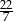Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej ﬁgury ma długość 33 cm, a jej pole jest równe 13 2 cm 2 . Oblicz objętość tego pudełka. Przyjmij przybliżenie równe 272 . Zapisz obliczenia.

Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.

Ukryj Podobne zadania

Obwód trapezu równoramiennego jest równy 56 cm, ramię ma długość 15 cm, a różnica długości podstaw wynosi 18 cm. Oblicz pole tego trapezu. Zapisz obliczenia.

Jeden z boków równoległoboku jest o 2,5 cm krótszy od drugiego boku. Obwód tego równoległoboku jest równy 29 cm. Oblicz długości jego boków.

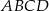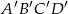Czworokąty ABCD i ′ ′ ′ ′ A B C D są podobne. Boki czworokąta 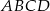ABCD mają długości 8 cm, 4 cm, 16 cm, 12 cm. Najdłuższy bok czworokąta 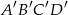A ′B′C′D ′ ma 20 cm. Jakie są długości pozostałych boków?

Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?

Ukryj Podobne zadania

Metalową kulę o promieniu 5 cm i stożek o średnicy 12 cm i wysokości 15 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?

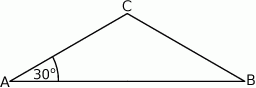
Kąt przy podstawie trójkąta równoramiennego 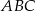ABC ma miarę 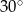∘ 30 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta ABC .

Z wierzchołka kąta prostego trójkąta prostokątnego 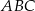ABC poprowadzono wysokość 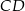, która podzieliła przeciwprostokątną 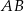na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).

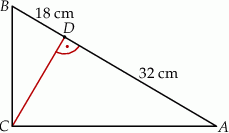
Oblicz pole trójkąta 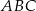ABC .

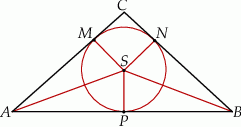
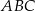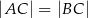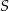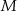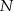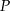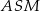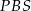W trójkąt równoramienny ABC ( |AC | = |BC | ) wpisano okrąg o środku . Punkty wspólne okręgu i trójkąta oznaczono literami , i . Uzasadnij, że trójkąty ASM i PBS są przystające.

Długości boków czworokąta opisano za pomocą wyrażeń algebraicznych, tak jak pokazano na rysunku.

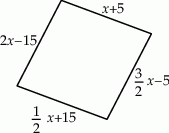
Uzasadnij, że jeśli obwód tego czworokąta jest równy 100 cm, to jest on rombem.

Wykaż, że jeżeli dwa kąty wpisane w okrąg są oparte na tym samym łuku, to mają równe miary.

Dwa spośród boków trójkąta mają długości 3 i 5. Zaznacz na osi liczbowej wszystkie liczby oznaczające możliwe długości trzeciego boku.

Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest prostokąt.

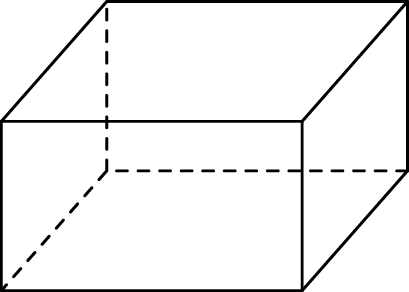
ZINFO-FIGURE

Jeden z boków tego prostokąta ma długość 16 cm, a długość jego przekątnej jest równa 20 cm. Przekątna najmniejszej ściany bocznej graniastosłupa ma długość 15 cm. Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.

Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.

Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest kwadratem o boku 5 cm, a druga – prostokątem o bokach 3 cm i 5 cm.

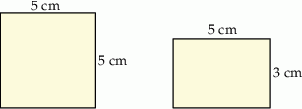
Oblicz sumę długości wszystkich krawędzi prostopadłościanu o takich wymiarach.

Ukryj Podobne zadania

Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest prostokątem o bokach 6 cm i 9 cm, a druga – prostokątem o bokach 9 cm i 12 cm.

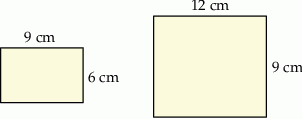
Oblicz pole powierzchni całkowitej prostopadłościanu o takich wymiarach.

Ile litrów wody można wlać do garnka w kształcie walca o średnicy 24 cm i wysokości 15 cm?

Suma wszystkich krawędzi ostrosłupa prawidłowego trójkątnego wynosi 72 cm. Oblicz długość krawędzi podstawy tego ostrosłupa, jeśli krawędź boczna ma długość 16 cm.

Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.

Dany jest graniastosłup prawidłowy czworokątny, w którym zaznaczone podstawy są kwadratami. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 1. jest równa 27 cm. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 2. jest równa 30 cm.

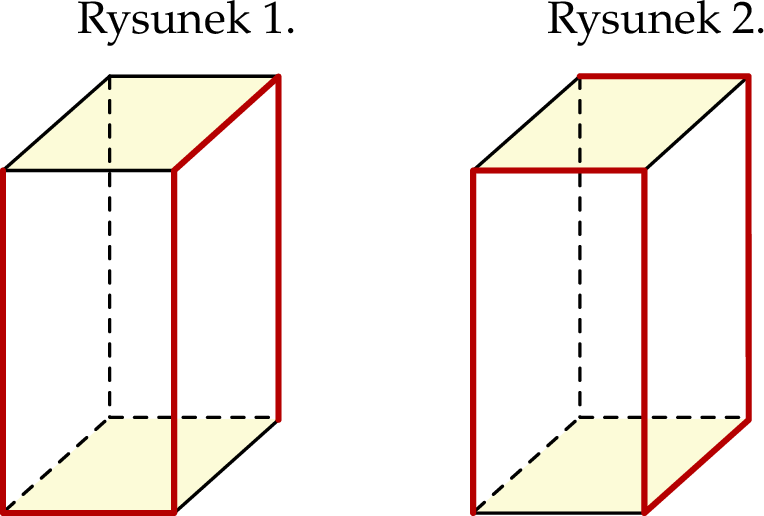
ZINFO-FIGURE

Oblicz objętość tego graniastosłupa.

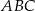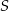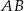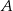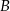Dany jest trójkąt ABC . Punkt jest środkiem boku tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów i od prostej 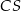są równe.

Ukryj Podobne zadania

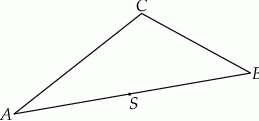
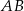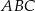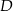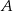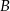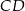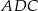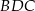Na boku trójkąta ABC wybrano punkt w ten sposób, że odległości punktów i od prostej są równe (zobacz rysunek). Wykaż, że trójkąty ADC i BDC mają równe pola.

Strona 3 z 15