Pod jakim kątem przecinają się proste 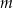 i
i  ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pod jakim kątem przecinają się proste 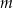 i
i  ?
?

Proste  i
i 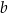 są równoległe. Półproste
są równoległe. Półproste 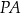 i
i 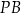 przecinają te proste, w punktach
przecinają te proste, w punktach 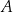 i
i 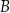 w wyniku czego tworzą z nimi kąty ostre o miarach podanych na rysunku.
w wyniku czego tworzą z nimi kąty ostre o miarach podanych na rysunku.
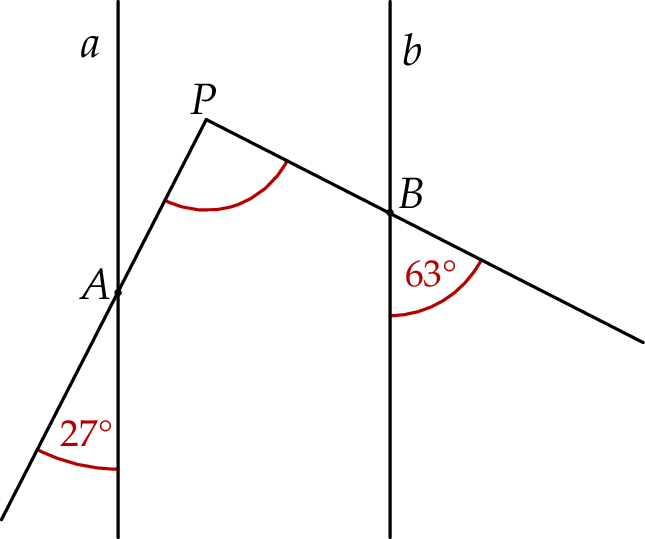
Uzasadnij, że kąt 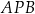 jest prosty.
jest prosty.
Pod jakim kątem przecinają się proste  i
i  ?
?
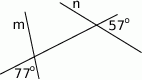
Pod jakim kątem przecinają się proste 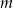 i
i  ?
?
Oblicz pole i obwód koła o promieniu 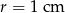 .
.
Oblicz pole i obwód koła o promieniu 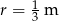 .
.
Oblicz pole i obwód koła o promieniu 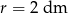 .
.
Oblicz pole i obwód koła o promieniu 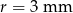 .
.
Oblicz pole i obwód koła o promieniu 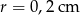 .
.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Z czterech ołowianych sześcianów o przekątnej długości 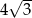 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
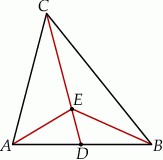
Na środkowej 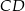 trójkąta
trójkąta 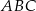 wybrano punkt
wybrano punkt 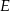 . Wykaż, że trójkąty
. Wykaż, że trójkąty 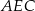 i
i 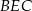 mają równe pola.
mają równe pola.
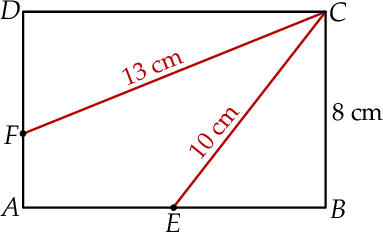
W prostokącie 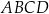 o polu
o polu 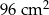 bok
bok 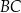 ma długość 8 cm. Na bokach
ma długość 8 cm. Na bokach 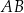 i
i 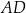 wybrano punkty
wybrano punkty 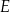 i
i 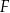 tak, że
tak, że 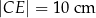 i
i 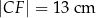 . Oblicz pole czworokąta
. Oblicz pole czworokąta 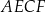 .
.
Z półkola o promieniu  wycięto półkole o średnicy
wycięto półkole o średnicy  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 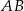 jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 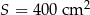 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 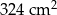 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły .
Punkt 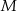 przyprostokątnej
przyprostokątnej 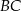 trójkąta prostokątnego
trójkąta prostokątnego 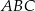 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 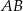 otrzymując punkt
otrzymując punkt 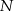 . Wykaż, że
. Wykaż, że 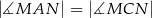 .
.
Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 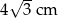 .
.
Dany jest trójkąt ostrokątny równoramienny 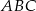 , w którym bok
, w którym bok 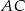 jest równy
jest równy 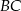 . Odcinek
. Odcinek 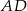 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 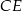 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt  jest równy kątowi
jest równy kątowi 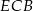 .
.
Narysuj w układzie współrzędnych czworokąt o wierzchołkach: 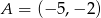 ,
, 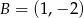 ,
, 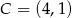 ,
, 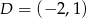 , a następnie oblicz jego pole i obwód.
, a następnie oblicz jego pole i obwód.
Narysuj w układzie współrzędnych czworokąt o wierzchołkach: 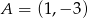 ,
, 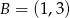 ,
, 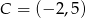 ,
, 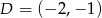 , a następnie oblicz jego pole i obwód.
, a następnie oblicz jego pole i obwód.
Na rysunku przedstawiono trapez równoramienny  , w którym
, w którym 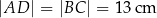 .
.
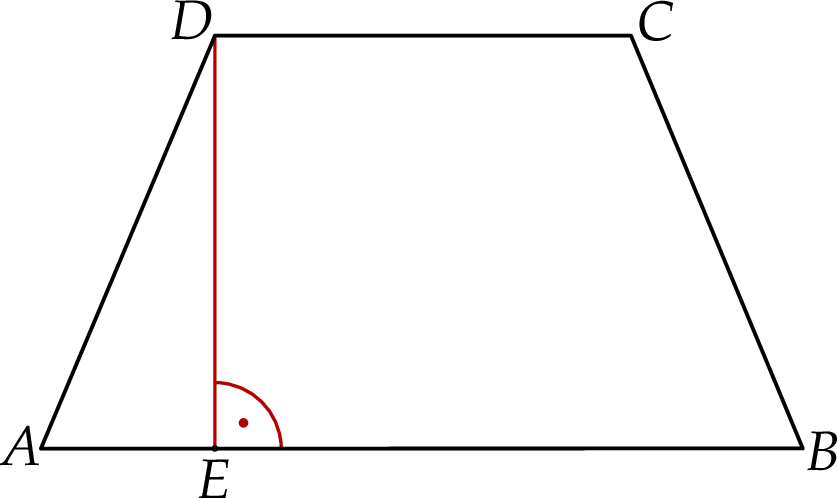
Wysokość 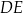 oraz krótsza podstawa
oraz krótsza podstawa 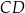 mają długość po 12 cm. Oblicz pole trapezu
mają długość po 12 cm. Oblicz pole trapezu 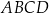 .
.
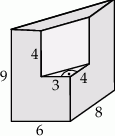
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
Podstawy trapezu równoramiennego 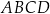 mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe
mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe 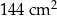 . Oblicz obwód trapezu
. Oblicz obwód trapezu 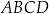 .
.
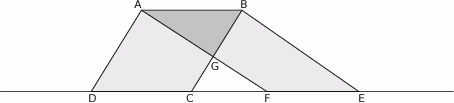
Na rysunku przedstawiono dwa równoległoboki 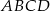 i
i 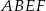 . Uzasadnij, że czworokąty
. Uzasadnij, że czworokąty 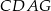 oraz
oraz 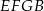 mają równe pola.
mają równe pola.
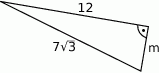
Oblicz długości odcinka  .
.
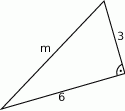
Oblicz długości odcinka  .
.
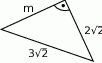
Oblicz długości odcinka  .
.
Oblicz długości boków prostokąta o obwodzie 1,1 dm którego boki są proporcjonalne do odcinków długości 4 cm i 7 cm.
Trójkąt równoboczny, kwadrat i sześciokąt foremny mają ten sam obwód długości 10cm. Oblicz pole każdej z tych figur. Która z nich ma największe pole, a która najmniejsze?
