W trapezie 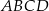 mamy
mamy 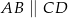 oraz
oraz 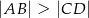 . Punkt
. Punkt 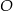 jest środkiem ramienia
jest środkiem ramienia 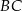 , a punkt
, a punkt 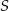 jest punktem wspólnym prostych
jest punktem wspólnym prostych 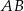
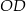 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 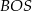 jest równe polu trójkąta
jest równe polu trójkąta 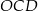 .
.
/Szkoła podstawowa/Geometria
Liczby 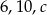 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Prosta 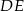 jest równoległa do boku
jest równoległa do boku 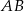 trójkąta
trójkąta 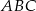 i przecina bok
i przecina bok 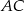 w punkcie
w punkcie 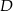 , bok
, bok 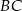 w punkcie
w punkcie 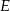 . Oblicz
. Oblicz 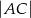 jeśli
jeśli 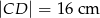 ,
, 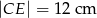 i
i 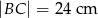 .
.
Prosta 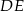 jest równoległa do boku
jest równoległa do boku 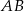 trójkąta
trójkąta 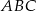 i przecina bok
i przecina bok 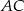 w punkcie
w punkcie 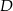 , bok
, bok 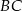 w punkcie
w punkcie 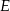 . Oblicz
. Oblicz 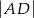 jeśli
jeśli 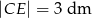 ,
, 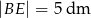 i
i 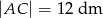 .
.
Prosta 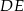 jest równoległa do boku
jest równoległa do boku 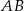 trójkąta
trójkąta 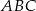 i przecina bok
i przecina bok 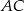 w punkcie
w punkcie 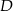 , bok
, bok 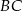 w punkcie
w punkcie 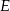 . Oblicz
. Oblicz 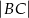 , jeśli
, jeśli 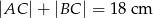 ,
, 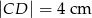 i
i 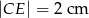 .
.
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
Oblicz pole trójkąta przedstawionego na rysunku.
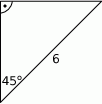
Oblicz pole trójkąta przedstawionego na rysunku.
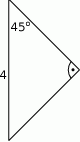
Na rysunku przedstawiono kwadrat 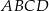 o polu
o polu 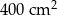 . Figurę tę podzielono na kwadrat
. Figurę tę podzielono na kwadrat 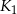 o polu
o polu 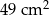 i kwadrat
i kwadrat 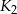 oraz figurę
oraz figurę 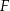 (patrz rysunek).
(patrz rysunek).
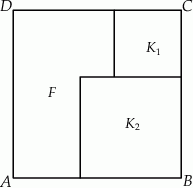
Oblicz obwód figury 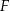 .
.
Na rysunku przedstawiono kwadrat 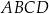 o polu
o polu 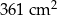 . Figurę tę podzielono na kwadrat
. Figurę tę podzielono na kwadrat 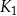 o polu
o polu 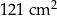 i kwadrat
i kwadrat 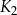 oraz figurę
oraz figurę 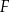 (patrz rysunek).
(patrz rysunek).
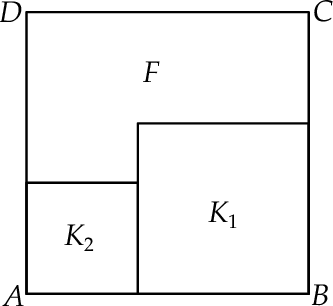
Oblicz obwód figury 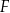 .
.
Bok 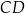 kwadratu
kwadratu 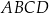 podzielono punktami
podzielono punktami 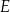 i
i 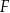 na trzy odcinki równej długości. Przez wierzchołek
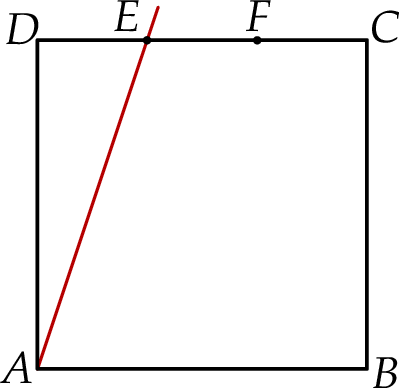
na trzy odcinki równej długości. Przez wierzchołek 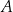 kwadratu i przez punkt
kwadratu i przez punkt 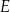 poprowadzono prostą (zobacz rysunek). Pole trójkąta
poprowadzono prostą (zobacz rysunek). Pole trójkąta 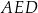 jest równe
jest równe 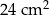 .
.
Oblicz pole kwadratu 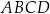 .
.
Oblicz pole i obwód trapezu przedstawionego na rysunku.
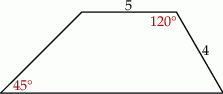
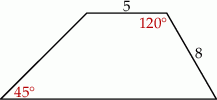
Oblicz pole i obwód trapezu przedstawionego na rysunku.
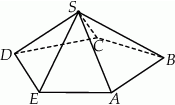
Dany jest ostrosłup o podstawie pięciokątnej 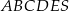 (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 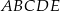 . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
W tabelce podano pola kwadratów. Ustal, które z nich mają boki o długościach wyrażonych liczbami całkowitymi.
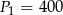 | 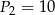 |
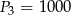 | 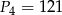 |
W tabelce podano pola kwadratów. Ustal, które z nich mają boki o długościach wyrażonych liczbami wymiernymi.
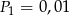 | 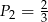 |
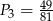 | 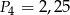 |
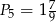 | 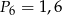 |
Jaka jest miara kąta  ?
?
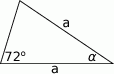
Jaka jest miara kąta  ?
?
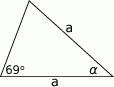
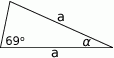
Jaka jest miara kąta  ?
?
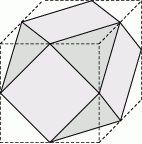
W kostce mającej kształt sześcianu o krawędzi długości 6 ścięto wszystkie naroża płaszczyznami przechodzącymi przez środki odpowiednich krawędzi (zobacz rysunek). Oblicz objętość otrzymanej bryły.
Paweł wyciął z kartonu trójkąt prostokątny 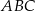 o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt  wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez  (rysunek II).
(rysunek II).
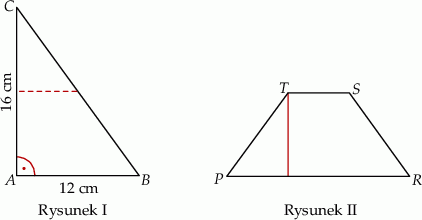
Oblicz różnicę obwodów trójkąta  i trapezu
i trapezu 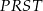 .
.
Karol wyciął z kartonu trójkąt prostokątny 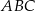 (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
(rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt 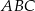 wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez 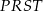 o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
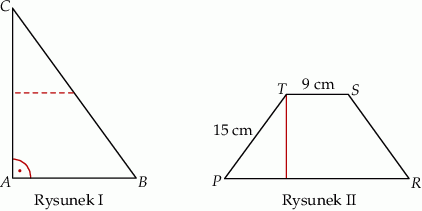
Oblicz różnicę obwodów trójkąta 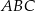 i trapezu
i trapezu 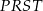 .
.
Wierzchołek 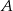 trójkąta ostrokątnego
trójkąta ostrokątnego 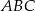 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 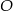 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 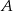 poprowadzono wysokość
poprowadzono wysokość 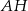 . Wykaż, że
. Wykaż, że 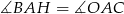 .
.
W czworokącie 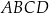 o polu
o polu 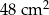 przekątna
przekątna 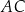 ma długość 8 cm i dzieli ten czworokąt na dwa trójkąty:
ma długość 8 cm i dzieli ten czworokąt na dwa trójkąty: 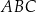 i
i 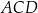 (zobacz rysunek). Wysokość trójkąta
(zobacz rysunek). Wysokość trójkąta 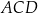 poprowadzona z wierzchołka
poprowadzona z wierzchołka 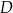 do prostej
do prostej 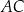 jest równa 2 cm.
jest równa 2 cm.
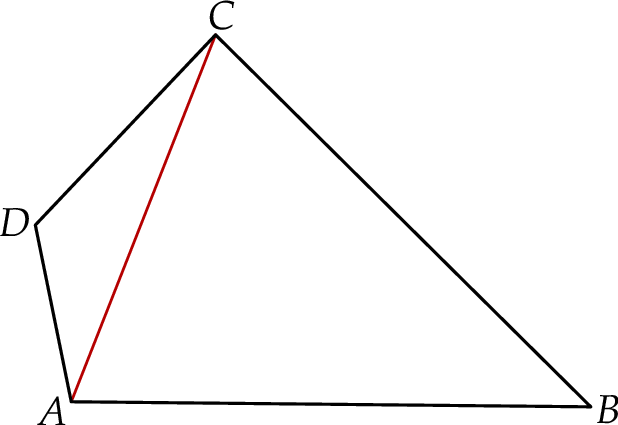
Oblicz wysokość trójkąta 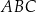 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 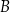 do prostej
do prostej 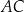 .
.
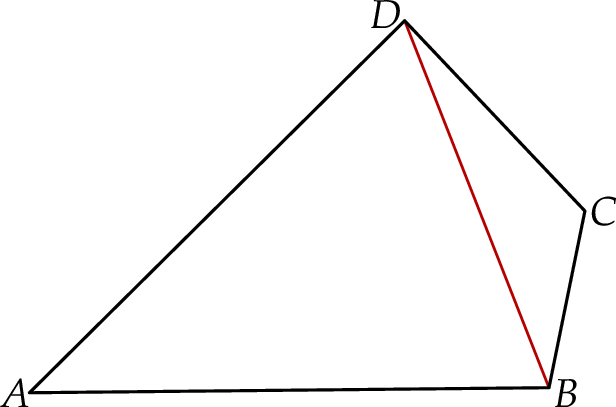
W czworokącie 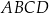 o polu
o polu 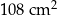 przekątna
przekątna 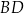 ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty:
ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty: 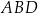 i
i 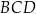 (zobacz rysunek). Wysokość trójkąta
(zobacz rysunek). Wysokość trójkąta 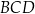 poprowadzona z wierzchołka
poprowadzona z wierzchołka 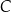 do prostej
do prostej 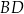 jest równa 3 cm.
jest równa 3 cm.
Oblicz wysokość trójkąta 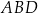 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 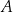 do prostej
do prostej 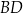 .
.
Prostokąt 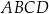 podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek).
podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek).
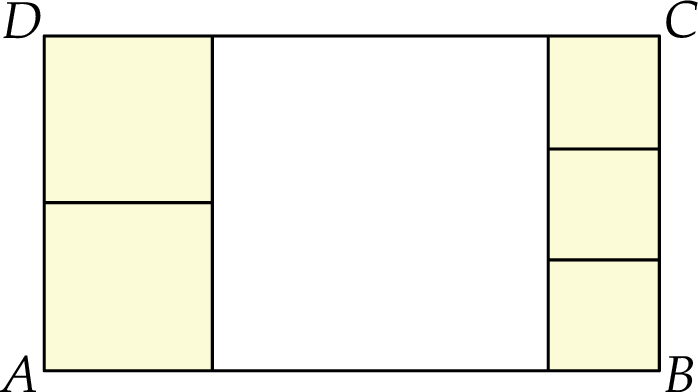
Uzasadnij, że pole dużego kwadratu jest większe niż połowa pola prostokąta 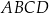 .
.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.
Oblicz pole prostokąta o wierzchołkach: 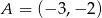 ,
, 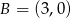 ,
, 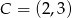 ,
, 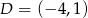 .
.
Oblicz pole prostokąta o wierzchołkach: 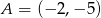 ,
, 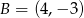 ,
, 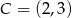 ,
, 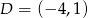 .
.
Oblicz pole prostokąta o wierzchołkach: 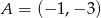 ,
, 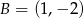 ,
, 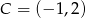 ,
, 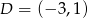 .
.
Oblicz pole prostokąta o wierzchołkach: 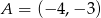 ,
, 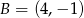 ,
, 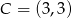 ,
, 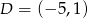 .
.
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 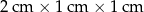 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
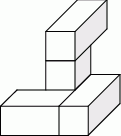
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 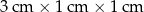 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
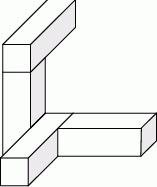
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?

