Różne/Układy równań - zadania z matematyki

/Studia/Algebra liniowa/Układy równań/Różne

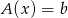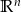Wykazać, że jeśli równanie liniowe A (x) = b w n R , ma dwa różne rozwiązania, to ma ich nieskończenie wiele.

Dla podanego odwzorowania liniowego wyznaczyć zbiór tych wektorów 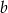, dla których równanie 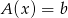A (x) = b ma rozwiązanie.

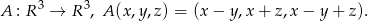
A : R 3 → R3, A (x,y,z) = (x − y,x + z,x − y + z ).

Ukryj Podobne zadania

Dla podanego odwzorowania liniowego wyznaczyć zbiór tych wektorów 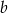, dla których równanie 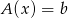A (x) = b ma rozwiązanie.

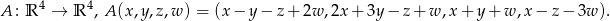
A : R 4 → R 4, A (x,y,z,w ) = (x − y− z+ 2w ,2x + 3y − z+ w ,x + y+ w,x − z − 3w ).

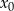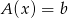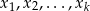Wykazać, że jeśli x 0 jest rozwiązaniem równania liniowego A (x) = b , a x1,x2,...,xk są rozwiazaniami równania liniowego jednorodnego stowarzyszonego, to 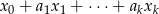x0 + a1x1 + ⋅⋅⋅+ akxk jest też rozwiązaniem równania .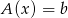