Punkty 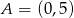 i
i 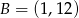 należą do wykresu funkcji
należą do wykresu funkcji 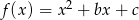 . Zapisz wzór funkcji w postaci ogólnej, kanonicznej i iloczynowej.
. Zapisz wzór funkcji w postaci ogólnej, kanonicznej i iloczynowej.
/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/2 niewiadome
Wykresy funkcji kwadratowych 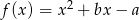 oraz
oraz 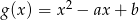 , gdzie
, gdzie 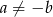 , przecinają się w punkcie leżącym na osi
, przecinają się w punkcie leżącym na osi 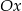 . Wiedząc, że osią symetrii wykresu funkcji
. Wiedząc, że osią symetrii wykresu funkcji 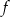 jest prosta o równaniu
jest prosta o równaniu 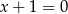 , oblicz
, oblicz 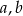 .
.
Wyznacz wszystkie wartości parametrów  i
i 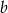 , dla których wykresy funkcji
, dla których wykresy funkcji
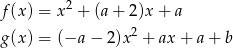
przecinają się w dwóch różnych punktach leżących na osi 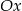 .
.
Dane są dwie funkcje kwadratowe 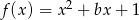 oraz
oraz 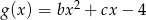 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów 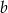 oraz
oraz  , tak aby wykresy funkcji miały wierzchołek w punkcie o odciętej -2.
, tak aby wykresy funkcji miały wierzchołek w punkcie o odciętej -2.
Wykresem funkcji kwadratowej 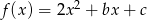 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 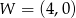 . Oblicz wartości współczynników
. Oblicz wartości współczynników 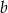 i
i  .
.
Wykresem funkcji kwadratowej 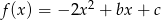 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 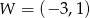 . Oblicz wartości współczynników
. Oblicz wartości współczynników 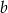 i
i  .
.
Wyznacz współczynniki  i
i 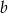 funkcji kwadratowej
funkcji kwadratowej 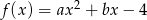 , jeśli współrzędne wierzchołka wynoszą
, jeśli współrzędne wierzchołka wynoszą 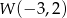 . Przedstaw trójmian w postaci iloczynowej.
. Przedstaw trójmian w postaci iloczynowej.

