Wyznacz wszystkie styczne do wykresu funkcji 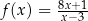 , które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
, które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
/Studia/Analiza/Funkcje/Badanie funkcji
Z punktu 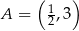 poprowadzono styczne do wykresu funkcji
poprowadzono styczne do wykresu funkcji 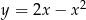 . Wyznacz równia tych stycznych.
. Wyznacz równia tych stycznych.
Na poniższym wykresie przedstawiono wykres pochodnej 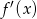 funkcji kwadratowej
funkcji kwadratowej 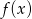 . Wykaż, że
. Wykaż, że 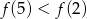 .
.
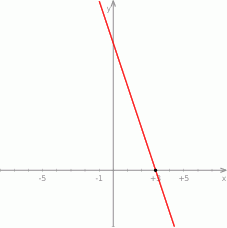
Dana jest funkcja
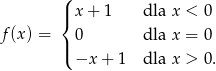
Wykaż, że funkcja ta nie jest ciągła w punkcie 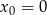 .
.
Oblicz pochodną funkcji 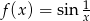 .
.
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 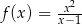 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 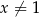 , poprowadzonej w punkcie
, poprowadzonej w punkcie 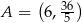 tego wykresu.
tego wykresu.
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 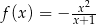 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 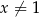 , poprowadzonej w punkcie
, poprowadzonej w punkcie 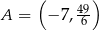 tego wykresu.
tego wykresu.
Dla jakich wartości parametru  parabola
parabola 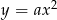 jest styczna do krzywej
jest styczna do krzywej 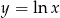 .
.
Wyznacz wartość największą i najmniejszą funkcji 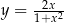 w przedziale
w przedziale 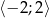 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 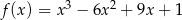 .
.
Wyznacz przedziały monotoniczności funkcji 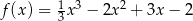 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 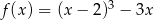 .
.
Oblicz granicę jednostronną 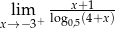 .
.
Oblicz granicę jednostronną 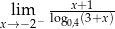 .
.
Dana jest funkcja 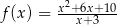 .
.
- Określ przedziały monotoniczności tej funkcji.
- Znajdź ekstrema lokalne funkcji
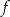 .
.
Oblicz pochodną funkcji 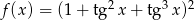 .
.
Dla jakich wartości parametru 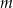 prosta
prosta 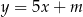 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 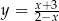 ?
?
Dla jakich wartości parametru 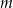 prosta
prosta 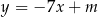 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 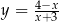 ?
?
Wyznacz punkty przegięcia wykresu funkcji 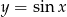 .
.
Wyznacz pole trójkąta, którego dwa boki zawierają się w asymptotach wykresu funkcji 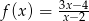 , a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie
, a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie 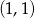 .
.
Funkcja 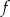 jest określona wzorem
jest określona wzorem 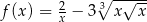 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 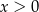 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 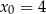 .
.
Wyznacz asymptoty funkcji 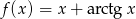 .
.
Wyznacz najmniejszą 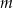 i największą
i największą 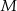 wartość funkcji
wartość funkcji 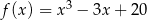 w przedziale
w przedziale 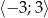 .
.
Dla jakich wartości parametrów  i
i 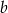 punkt
punkt 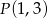 jest punktem przegięcia krzywej
jest punktem przegięcia krzywej 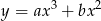 ?
?
Wyznacz równania wszystkich stycznych do wykresu funkcji 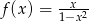 ,
, 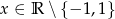 nachylonych do osi
nachylonych do osi 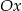 pod kątem
pod kątem 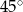 .
.

