Wykaż, że jeżeli funkcje 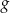 i
i 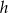 są określone w tym samym zbiorze i są rosnące, to funkcja określona wzorem
są określone w tym samym zbiorze i są rosnące, to funkcja określona wzorem 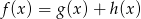 jest rosnąca.
jest rosnąca.
/Studia/Analiza/Funkcje/Badanie funkcji
Korzystając ze wzoru 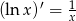 oblicz pochodną funkcji
oblicz pochodną funkcji 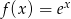 .
.
Napisz równanie stycznej do krzywej 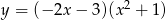 w punkcie
w punkcie 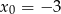 .
.
Wyznacz asymptoty funkcji 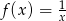 .
.
Uzasadnij, że nie istnieje granica 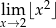 .
.
Uzasadnij, że nie istnieje granica 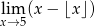 .
.
Napisz równanie stycznej do krzywej 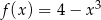 wiedząc, że jest ona równoległa do prostej
wiedząc, że jest ona równoległa do prostej 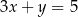 .
.
Funkcja 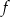 określona jest wzorem
określona jest wzorem 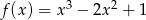 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 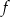 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 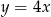 .
.
Funkcja 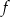 określona jest wzorem
określona jest wzorem 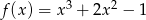 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 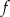 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 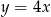 .
.
Funkcja 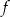 jest określona wzorem
jest określona wzorem 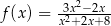 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 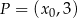 należy do wykresu funkcji
należy do wykresu funkcji 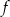 . Oblicz
. Oblicz 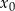 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 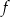 w punkcie
w punkcie 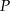 .
.
Funkcja 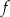 jest określona wzorem
jest określona wzorem 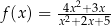 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 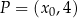 należy do wykresu funkcji
należy do wykresu funkcji 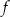 . Oblicz
. Oblicz 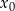 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 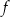 w punkcie
w punkcie 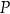 .
.
Funkcje 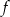 i
i 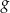 są określone wzorami:
są określone wzorami: 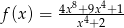 i
i 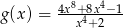 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wykaż, że
. Wykaż, że 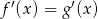 .
.
Przedstaw funkcję 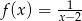 , określoną w zbiorze
, określoną w zbiorze 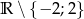 , jako sumę funkcji parzystej i nieparzystej.
, jako sumę funkcji parzystej i nieparzystej.
Wyznacz asymptoty funkcji 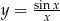 .
.
Oblicz pochodną funkcji 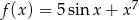 .
.
Oblicz granicę 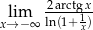 .
.
Wyznacz ekstrema lokalne funkcji 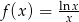 .
.
Korzystając ze wzoru 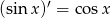 oblicz pochodną funkcji
oblicz pochodną funkcji 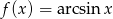 .
.
Korzystając ze wzoru 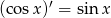 oblicz pochodną funkcji
oblicz pochodną funkcji 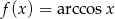 .
.
Wyznacz ekstrema funkcji 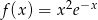 .
.
Oblicz granicę 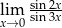 .
.
Oblicz pochodną funkcji 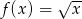 .
.
Oblicz pochodną funkcji 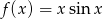 .
.
Wyznacz wszystkie wartości parametru  , dla których prosta o równaniu
, dla których prosta o równaniu 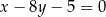 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 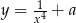 .
.
Zbadać czy istnieje granica 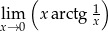 .
.

