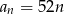Jeżeli suma miar kąta środkowego i kąta wpisanego opartych na tym samym łuku jest równa 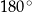 , to kąty te są oparte na
, to kąty te są oparte na
A) 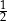 okręgu B)
okręgu B)  okręgu C)
okręgu C)  okręgu D)
okręgu D)  okręgu
okręgu
/Szkoła średnia/Zadania testowe
Liczba 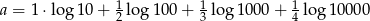 jest równa
jest równa
A) 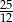 B)
B) 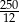 C) 4 D) 11110
C) 4 D) 11110
Liczba 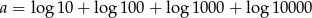 jest równa
jest równa
A) 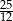 B) 10 C) 4 D) 11110
B) 10 C) 4 D) 11110
Liczba 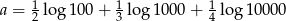 jest równa
jest równa
A) 3 B) 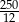 C) 4 D) 11100
C) 4 D) 11100
Jeśli 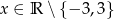 , to wyrażenie
, to wyrażenie 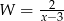 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 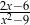 B)
B) 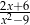 C)
C) 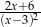 D)
D) 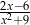
Jeśli 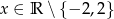 , to wyrażenie
, to wyrażenie 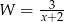 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 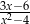 B)
B) 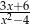 C)
C) 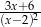 D)
D) 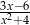
Jeśli 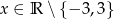 , to wyrażenie
, to wyrażenie 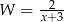 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 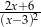 B)
B) 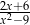 C)
C) 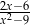 D)
D) 
Każda liczba  należąca do przedziału otwartego
należąca do przedziału otwartego 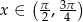 spełnia nierówność
spełnia nierówność
A) 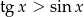 B)
B) 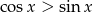 C)
C) 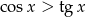 D)
D) 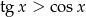
Każda liczba  należąca do przedziału otwartego
należąca do przedziału otwartego 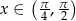 spełnia nierówność
spełnia nierówność
A) 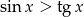 B)
B) 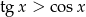 C)
C) 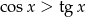 D)
D) 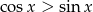
Czworokąty 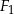 i
i 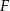 są podobne. Pole czworokąta
są podobne. Pole czworokąta 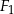 jest o 36% mniejsze od pola czworokąta
jest o 36% mniejsze od pola czworokąta 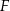 . Obwód czworokąta
. Obwód czworokąta 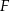 jest większy od obwodu czworokąta
jest większy od obwodu czworokąta 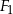 o:
o:
A) 20% B) 25% C) 36% D) 18%
Dane są punkty o współrzędnych 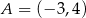 oraz
oraz 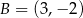 . Średnica okręgu opisanego na kwadracie o boku
. Średnica okręgu opisanego na kwadracie o boku 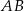 jest równa
jest równa
A) 12 B) 6 C) 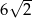 D)
D) 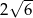
Proste o równaniach 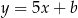 i
i 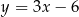 przecinają się w punkcie leżącym na osi
przecinają się w punkcie leżącym na osi 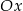 . Zatem
. Zatem
A) 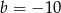 B)
B) 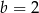 C)
C) 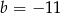 D)
D) 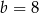
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 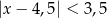 B)
B) 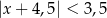 C)
C) 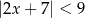 D)
D) 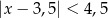
Wskaż nierówność, której ilustracją jest przedział:
![]()
A) 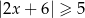 B)
B) 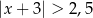 C)
C) 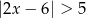 D)
D) 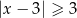
Na osi liczbowej zaznaczono sumę przedziałów.

Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A) 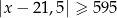 B)
B) 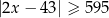
C) 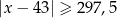 D)
D) 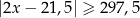
Na osi liczbowej zaznaczono sumę przedziałów.

Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A) 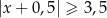 B)
B) 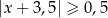
C) 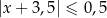 D)
D) 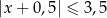
Na osi liczbowej zaznaczono sumę przedziałów.

Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A) 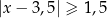 B)
B) 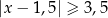
C) 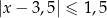 D)
D) 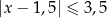
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 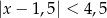 B)
B) 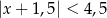 C)
C) 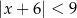 D)
D) 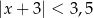
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 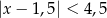 B)
B) 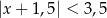 C)
C) 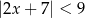 D)
D) 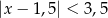
Ile wyrazów ma ciąg geometryczny 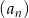 , w którym
, w którym 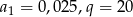 , natomiast ostatni wyraz jest równy 4000?
, natomiast ostatni wyraz jest równy 4000?
A) 3 B) 4 C) 5 D) 6
Ile wyrazów ma ciąg geometryczny 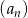 , w którym
, w którym 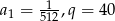 , natomiast ostatni wyraz jest równy 5000?
, natomiast ostatni wyraz jest równy 5000?
A) 3 B) 4 C) 5 D) 6
Ile wyrazów ma ciąg geometryczny 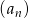 , w którym
, w którym 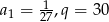 , natomiast ostatni wyraz jest równy 1000?
, natomiast ostatni wyraz jest równy 1000?
A) 3 B) 4 C) 5 D) 6
Koło ma promień równy 3. Obwód wycinka tego koła o kącie środkowym 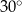 jest równy
jest równy
A) 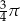 B)
B) 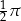 C)
C) 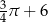 D)
D) 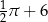
Koło ma promień równy 4. Obwód wycinka tego koła o kącie środkowym 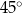 jest równy
jest równy
A) 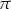 B)
B) 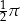 C)
C) 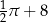 D)
D) 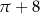
Koło ma promień równy 12. Obwód wycinka tego koła o kącie środkowym 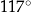 jest równy
jest równy
A) 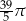 B)
B) 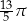 C)
C) 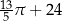 D)
D) 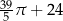
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 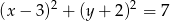 .
.
A) 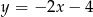 B)
B) 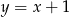 C)
C) 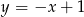 D)
D) 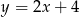
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 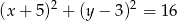 .
.
A) 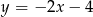 B)
B) 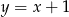 C)
C) 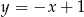 D)
D) 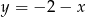
Dany jest okrąg o równaniu 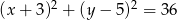 . Jedna ze średnic okręgu zawarta jest w prostej
. Jedna ze średnic okręgu zawarta jest w prostej
A) 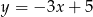 B)
B) 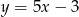 C)
C) 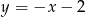 D)
D) 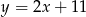
Na rysunku przedstawiono bryłę zbudowaną z walca, stożka i półkuli. Wysokość walca jest równa  i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
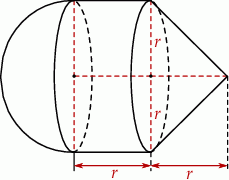
Objętość tej bryły jest równa
A) 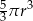 B)
B) 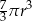 C)
C) 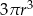 D)
D) 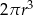
Liczbą odwrotną do liczby 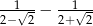 jest liczba
jest liczba
A) 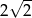 B)
B) 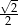 C)
C) 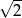 D) 2
D) 2
Liczbą odwrotną do liczby 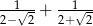 jest liczba
jest liczba
A) 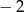 B) 2 C)
B) 2 C) 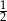 D)
D) 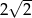
Liczba odwrotna do liczby 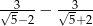 jest liczba
jest liczba
A) 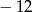 B)
B) 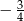 C)
C) 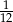 D)
D) 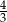
Równanie 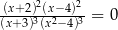
A) ma cztery różne rozwiązania: 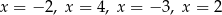 .
.
B) ma trzy różne rozwiązania: 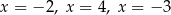 .
.
C) ma dwa różne rozwiązania: 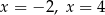 .
.
D) ma jedno rozwiązanie: 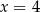 .
.
Pięciowyrazowy ciąg 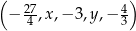 jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
A) 81 B) 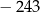 C)
C) 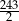 D)
D) 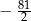
Dla 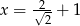 oraz
oraz 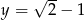 wartość wyrażenia
wartość wyrażenia 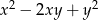 jest równa
jest równa
A) 4 B) 1 C) 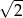 D)
D) 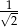
Dla 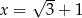 oraz
oraz 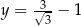 wartość wyrażenia
wartość wyrażenia 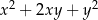 jest równa
jest równa
A) 3 B) 12 C) 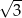 D)
D) 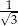
Dana jest funkcja liniowa określona wzorem 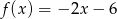 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 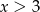 B)
B) 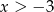 C)
C) 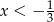 D)
D) 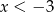
Funkcja liniowa 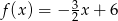 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 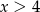 B)
B) 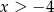 C)
C) 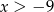 D)
D) 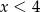
Funkcja 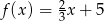 przyjmuje wartości dodatnie w przedziale:
przyjmuje wartości dodatnie w przedziale:
A) 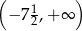 B)
B) 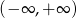 C)
C) 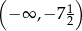 D)
D) 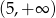
Funkcja liniowa określona wzorem 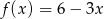 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 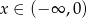 B)
B) 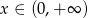 C)
C) 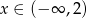 D)
D) 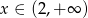
Dana jest funkcja liniowa określona wzorem 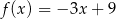 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 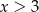 B)
B) 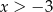 C)
C) 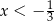 D)
D) 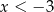
Dane są dwa prostopadłościany podobne: 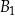 oraz
oraz 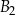 . Objętość prostopadłościanu
. Objętość prostopadłościanu 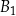 jest równa
jest równa 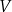 , a objętość prostopadłościanu
, a objętość prostopadłościanu 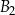 jest równa
jest równa 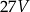 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 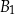 jest równe
jest równe 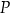 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 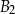 jest równe
jest równe
A) 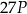 , , | B) 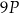 , , | C) 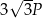 |
ponieważ stosunek pól powierzchni całkowitych prostopadłościanów podobnych jest równy
| 1) | stosunkowi objętości tych prostopadłościanów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku objętości tych prostopadłościanów. |
| 3) | kwadratowi stosunku długości odcinków odpowiadających w obu prostopadłościanach. |
Rozwiązaniem nierówności 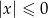 jest
jest
A) 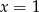 B)
B) 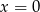 C)
C) 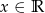 D)
D) 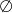
Rozwiązaniem nierówności 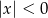 jest
jest
A) 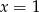 B)
B) 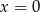 C)
C) 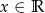 D)
D) 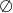
Zbiorem rozwiązań nierówności 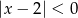 jest
jest
A) 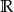 B)
B) 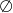 C)
C) 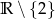 D)
D) 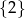
Zbiór rozwiązań nierówności 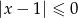 to
to
A) 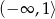 B)
B) 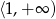 C)
C) 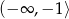 D)
D) 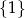
Zbiór rozwiązań nierówności 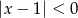 to
to
A) 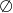 B)
B) 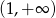 C)
C) 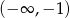 D)
D) 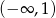
Rozwiązaniem nierówności 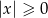 jest
jest
A) 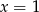 B)
B) 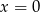 C)
C) 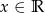 D)
D) 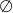
Wzór ogólny ciągu arytmetycznego, w którym 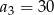 i
i 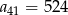 , to
, to
A) 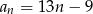 B)
B) 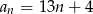 C)
C) 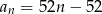 D)
D)