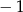Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste?
A) 16 B) 20 C) 24 D) 25
/Szkoła średnia/Zadania testowe
Liczb dwucyfrowych większych od 50 o nieparzystych cyfrach jest
A) 12 B) 25 C) 49 D) 15
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których pierwsza cyfra jest parzysta, a druga nieparzysta?
A) 16 B) 20 C) 24 D) 25
Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 90 B) 81 C) 82 D) 80
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są nieparzyste?
A) 16 B) 20 C) 24 D) 25
Pole rombu jest równe 32, a kąt ostry ma miarę 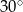 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 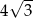 C)
C) 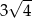 D) 4
D) 4
Pole rombu jest równe 50, a kąt ostry ma miarę 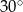 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 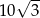 B) 5 C) 10 D)
B) 5 C) 10 D) 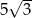
Pole rombu jest równe 18, a kąt ostry ma miarę 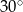 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 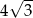 C)
C) 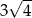 D) 4
D) 4
W każdym ostrosłupie prawidłowym czworokątnym kąt dwuścienny między ścianami bocznymi ma miarę
A) większą od 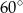 i mniejszą od
i mniejszą od 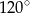 B) większą od
B) większą od 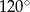 i mniejszą od
i mniejszą od 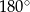
C) równą 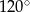 D) większą od
D) większą od 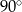 i mniejszą od
i mniejszą od 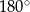
Liczba rozwiązań równania 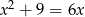 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Wyrażenie 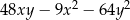 może być przekształcone do postaci
może być przekształcone do postaci
A) 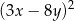 B)
B) 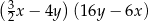 C)
C) 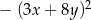 D)
D) 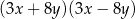
Prosta dana równaniem 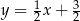 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji
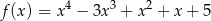
w punkcie
A) 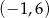 B)
B) 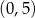 C)
C) 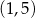 D)
D) 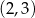
Funkcja 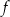 jest określona wzorem
jest określona wzorem 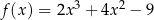 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Prosta o równaniu
. Prosta o równaniu 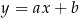 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 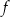 w punkcie
w punkcie 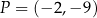 . Współczynnik
. Współczynnik  w równaniu tej stycznej jest równy
w równaniu tej stycznej jest równy
A) 8 B)  C)
C)  D)
D) 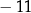
Prosta dana równaniem 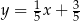 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 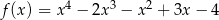 w punkcie
w punkcie
A) 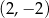 B)
B) 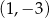 C)
C) 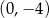 D)
D) 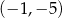
Dany jest równoramienny trójkąt  o kącie przy podstawie
o kącie przy podstawie 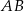 równym
równym 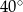 . Punkt
. Punkt 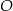 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 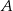 i
i 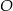 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 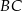 w punkcie
w punkcie 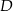 . Jeśli miara kąta
. Jeśli miara kąta 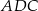 jest równa
jest równa  , to
, to
A) 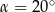 B)
B) 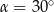 C)
C) 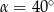 D)
D) 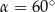
Dany jest równoramienny trójkąt 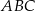 o kącie przy podstawie
o kącie przy podstawie 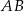 równym
równym 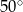 . Punkt
. Punkt 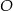 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 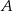 i
i 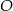 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 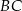 w punkcie
w punkcie 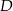 . Jeśli miara kąta
. Jeśli miara kąta 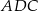 jest równa
jest równa  , to
, to
A) 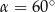 B)
B) 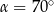 C)
C) 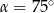 D)
D) 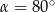
Dany jest równoramienny trójkąt 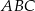 o kącie przy podstawie
o kącie przy podstawie 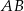 równym
równym 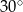 . Punkt
. Punkt 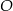 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 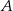 i
i 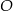 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 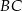 w punkcie
w punkcie 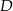 . Jeśli miara kąta
. Jeśli miara kąta 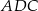 jest równa
jest równa  , to
, to
A) 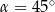 B)
B) 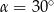 C)
C) 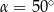 D)
D) 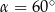
Jeżeli 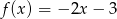 i
i 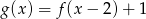 , to funkcja
, to funkcja 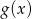 jest równa
jest równa
A) 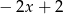 B)
B) 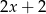 C)
C) 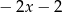 D)
D) 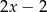
Jeżeli 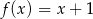 i
i 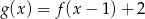 , to funkcja
, to funkcja 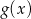 jest równa
jest równa
A) 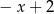 B)
B) 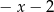 C)
C) 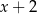 D)
D) 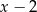
Jeżeli 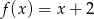 i
i 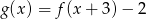 , to funkcja
, to funkcja 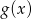 jest równa
jest równa
A) 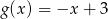 B)
B) 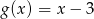 C)
C) 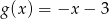 D)
D) 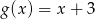
Przekątna sześcianu ma długość 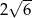 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 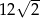 B)
B) 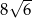 C)
C) 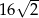 D) 48
D) 48
Przekątna sześcianu jest równa 6. Wynika stąd, że objętość tego sześcianu jest równa
A) 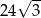 B) 72 C)
B) 72 C) 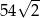 D)
D) 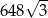
Przekątna sześcianu ma długość 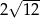 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 64 B) 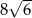 C)
C) 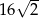 D) 48
D) 48
Przekątna sześcianu ma długość 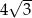 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 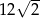 B)
B) 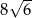 C)
C) 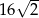 D) 64
D) 64
Przekątna sześcianu ma długość 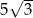 . Wtedy objętość tego sześcianu jest równa
. Wtedy objętość tego sześcianu jest równa
A) 125 B) 75 C) 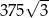 D)
D) 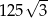
Przekątna sześcianu jest równa 9. Wynika stąd, że objętość tego sześcianu jest równa
A) 243 B) 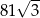 C)
C) 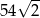 D)
D) 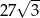
Iloczyn pierwiastków równania 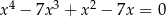 jest równy
jest równy
A) 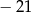 B) 14 C)
B) 14 C) 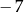 D) 0
D) 0
Liczbą wymierną nie jest liczba
A) 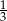 B)
B) 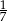 C)
C) 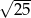 D)
D) 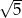
Liczbą wymierną nie jest liczba
A) 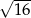 B)
B) 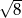 C)
C) 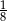 D)
D) 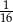
Liczbą wymierną nie jest liczba
A) 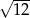 B)
B) 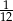 C)
C) 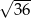 D)
D) 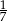
W ciągu arytmetycznym 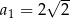 i
i 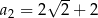 . Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
. Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
A) 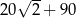 B)
B) 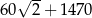 C)
C) 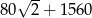 D)
D) 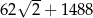
Granica 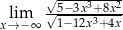
A) nie istnieje. B) jest liczbą dodatnią.
C) jest liczbą ujemną. D) jest równa 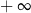 .
.
Największą liczbą całkowitą należącą do dziedziny funkcji 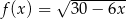 jest
jest
A) 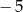 B)
B) 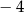 C) 5 D) 6
C) 5 D) 6
Największą liczbą całkowitą należącą do dziedziny funkcji 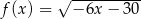 jest
jest
A) 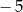 B)
B) 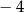 C) 5 D) 6
C) 5 D) 6
Największą liczbą całkowitą należącą do dziedziny funkcji 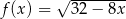 jest
jest
A) 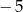 B)
B) 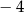 C) 5 D) 4
C) 5 D) 4
Najmniejszą liczbą całkowitą należącą do dziedziny funkcji 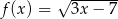 jest liczba
jest liczba
A) 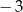 B)
B) 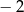 C) 2 D) 3
C) 2 D) 3
Zbiorem rozwiązań nierówności 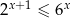 jest przedział
jest przedział
A) 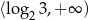 B)
B) 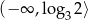 C)
C) 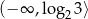 D)
D) 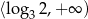
Punkt 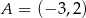 jest końcem odcinka
jest końcem odcinka 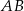 , a punkt
, a punkt 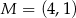 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 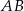 jest równa
jest równa
A) 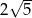 B)
B) 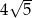 C)
C) 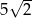 D)
D) 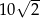
Punkt 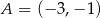 jest końcem odcinka
jest końcem odcinka 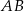 , a punkt
, a punkt 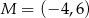 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 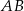 jest równa
jest równa
A) 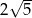 B)
B) 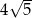 C)
C) 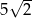 D)
D) 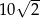
Ile jest liczb naturalnych pięciocyfrowych, w których iloczyn cyfr jest równy 0?
A) 59049 B) 30951 C) 3439 D) 6561
Ciąg 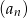 jest określony wzorem
jest określony wzorem 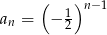 dla
dla 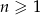 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 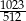 B)
B) 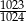 C)
C) 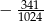 D)
D) 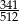
Para liczb 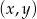 , która spełnia równanie
, która spełnia równanie 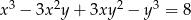 to
to
A) 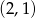 B)
B) 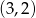 C)
C) 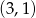 D)
D) 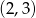
Największa wartość funkcji 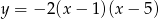 wynosi
wynosi
A) 2 B) 5 C) 8 D) 1
Największa wartość funkcji 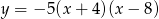 wynosi
wynosi
A) 140 B) 150 C) 160 D) 180
Najmniejsza wartość funkcji 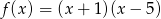 wynosi
wynosi
A) 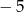 B) 5 C)
B) 5 C) 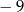 D)
D)