Wartość wyrażenia 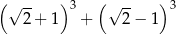 jest równa
jest równa
A) 14 B) 7 C) 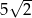 D)
D) 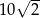
/Szkoła średnia/Zadania testowe
Wykresy funkcji 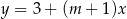 i
i 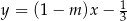 są prostopadłe. Zatem
są prostopadłe. Zatem 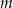
A) jest liczbą niewymierną B) jest liczbą ujemną
C) jest liczbą naturalną D) jest liczbą wymierną
Wykresy funkcji 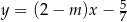 i
i 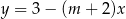 są prostopadłe. Zatem
są prostopadłe. Zatem 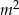
A) jest liczbą parzystą B) jest liczbą wymierną
C) jest równe 0 D) jest liczbą niewymierną
Funkcja liniowa 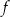 jest określona wzorem
jest określona wzorem 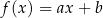 , gdzie
, gdzie  i
i 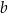 są pewnymi liczbami rzeczywistymi. Wykres tej funkcji przechodzi przez punkt
są pewnymi liczbami rzeczywistymi. Wykres tej funkcji przechodzi przez punkt 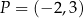 . Liczba
. Liczba  oraz liczba
oraz liczba 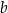 we wzorze funkcji
we wzorze funkcji 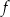 nie mogą spełniać warunku:
nie mogą spełniać warunku:
A) 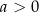 i
i 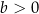 B)
B) 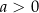 i
i 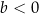 C)
C) 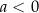 i
i 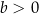 D)
D) 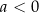 i
i 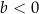
Wiadomo, że 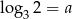 oraz
oraz 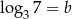 . Zatem
. Zatem 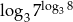 jest równy
jest równy
A) 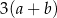 B)
B) 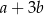 C)
C) 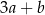 D)
D) 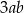
Spośród poniższych nierówności wskaż tę, którą spełniają wszystkie liczby całkowite.
A) 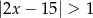 B)
B) 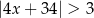 C)
C) 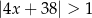 D)
D) 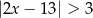
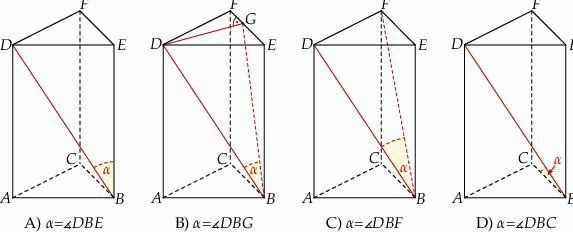
Kąt nachylenia przekątnej ściany bocznej graniastosłupa prawidłowego trójkątnego do sąsiedniej ściany bocznej przedstawiono na rysunku
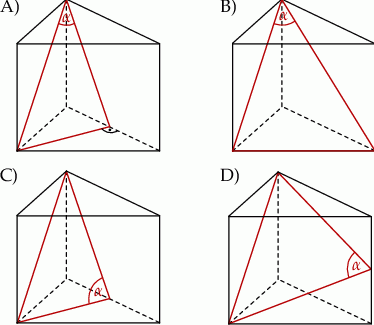
Dany jest graniastosłup prawidłowy trójkątny 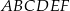 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 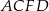 i przekątną
i przekątną 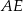 ściany bocznej
ściany bocznej 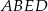 tego graniastosłupa?
tego graniastosłupa?
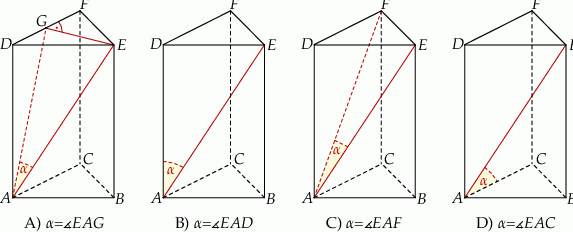
Dany jest graniastosłup prawidłowy trójkątny 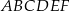 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 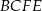 i przekątną
i przekątną 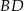 ściany bocznej
ściany bocznej 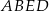 tego graniastosłupa?
tego graniastosłupa?
Promień okręgu o równaniu 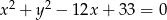 ma długość
ma długość
A) 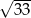 B)
B) 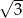 C) 3 D) 6
C) 3 D) 6
Promień okręgu danego równaniem 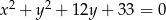 ma długość
ma długość
A) 3 B) 6 C) 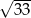 D)
D) 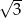
Promień okręgu danego równaniem 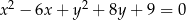 ma długość
ma długość
A) 2 B) 4 C) 9 D) 16
Promień okręgu danego równaniem 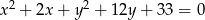 ma długość
ma długość
A) 2 B) 4 C) 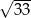 D)
D) 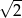
Promień okręgu danego równaniem 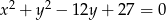 ma długość
ma długość
A) 3 B) 9 C) 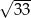 D)
D) 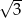
Różnica długości podstaw trapezu równoramiennego o kącie ostrym 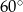 i ramieniu długości 12 może być równa
i ramieniu długości 12 może być równa
A) 6 B) 8 C) 9 D) 12
Dany jest ciąg geometryczny o wyrazie ogólnym 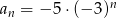 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -135 B) -45 C) 45 D) 135
Dany jest ciąg geometryczny o wyrazie ogólnym 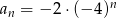 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -128 B) -32 C) 128 D) 32
Dany jest ciąg geometryczny o wyrazie ogólnym 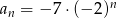 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -28 B) 56 C) -56 D) 28
Jeśli 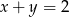 i
i 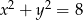 , to
, to 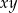 równa się
równa się
A) 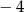 B) 2 C) 4 D)
B) 2 C) 4 D) 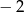
Wykres funkcji 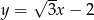 tworzy z osią
tworzy z osią 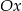 kąt rozwarty o mierze
kąt rozwarty o mierze
A) 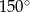 B)
B) 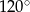 C)
C) 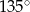 D)
D) 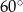
Wykres funkcji 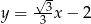 tworzy z osią
tworzy z osią 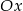 kąt rozwarty o mierze
kąt rozwarty o mierze
A) 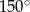 B)
B) 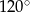 C)
C) 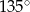 D)
D) 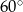
Wykres funkcji 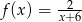 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 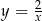 o 6 jednostek
o 6 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Aby otrzymać wykres funkcji 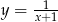 należy wykres funkcji
należy wykres funkcji 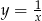 przesunąć o 1 jednostkę
przesunąć o 1 jednostkę
A) w dół B) w górę C) w prawo D) w lewo
Wykres funkcji 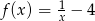 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 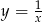 o 4 jednostki
o 4 jednostki
A) w lewo B) w prawo C) w górę D) w dół
Wykres funkcji 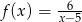 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 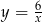 o 5 jednostek
o 5 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Ciąg arytmetyczny 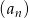 określony jest wzorem
określony jest wzorem 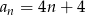 . Zatem suma
. Zatem suma 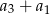 jest równa
jest równa
A) 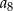 B)
B) 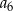 C)
C) 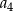 D)
D) 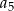
Ciąg arytmetyczny 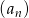 określony jest wzorem
określony jest wzorem 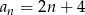 . Zatem suma
. Zatem suma 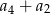 jest równa
jest równa
A) 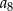 B)
B) 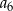 C)
C) 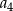 D)
D) 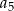
Ciąg arytmetyczny 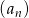 określony jest wzorem
określony jest wzorem 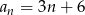 . Zatem suma
. Zatem suma 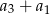 jest równa
jest równa
A) 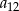 B)
B) 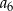 C)
C) 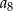 D)
D) 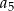
W układzie współrzędnych na płaszczyźnie dany jest odcinek 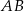 o końcach w punktach
o końcach w punktach 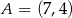 ,
, 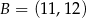 . Punkt
. Punkt 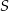 leży wewnątrz odcinka
leży wewnątrz odcinka 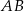 oraz
oraz 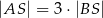 . Wówczas
. Wówczas
A) 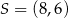 B)
B) 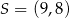 C)
C) 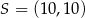 D)
D) 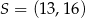
W układzie współrzędnych na płaszczyźnie dany jest odcinek 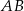 o końcach w punktach
o końcach w punktach 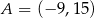 ,
, 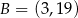 . Punkt
. Punkt 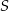 leży wewnątrz odcinka
leży wewnątrz odcinka 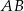 oraz
oraz 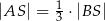 . Wówczas
. Wówczas
A) 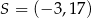 B)
B) 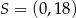 C)
C) 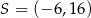 D)
D) 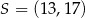
Odcinek 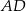 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 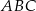 poprowadzoną do ramienia
poprowadzoną do ramienia 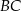 .
.
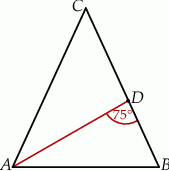
Jeżeli 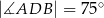 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 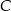 jest równa
jest równa
A) 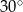 B)
B) 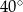 C)
C) 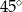 D)
D) 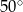
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 16 B) 20 C) 25 D) 30
Ze zbioru 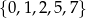 losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
A) 20 B) 16 C) 12 D) 10
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 17 B) 18 C) 19 D) 20
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są większe od 4 jest
A) 16 B) 20 C) 25 D) 30
Liczba 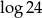 jest równa
jest równa
A) 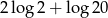 B)
B) 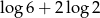 C)
C) 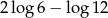 D)
D) 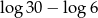
Liczba 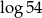 jest równa
jest równa
A) 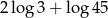 B)
B) 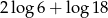 C)
C) 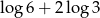 D)
D) 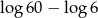
Liczba 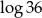 jest równa
jest równa
A) 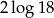 B)
B) 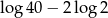 C)
C) 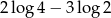 D)
D) 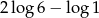
Liczba 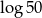 jest równa
jest równa
A) 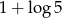 B)
B) 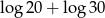 C)
C) 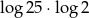 D)
D) 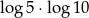
Liczba 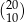 jest podzielna przez
jest podzielna przez
A) 5 B) 33 C) 221 D) 51
Liczba 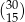 jest podzielna przez
jest podzielna przez
A) 7 B) 55 C) 143 D) 85
Objętość ostrosłupa prawidłowego czworokątnego jest równa 270, a pole jego podstawy jest równe 81. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 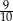 B)
B) 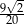 C)
C) 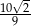 D)
D) 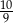
Objętość ostrosłupa prawidłowego czworokątnego jest równa 84, a pole jego podstawy jest równe 36. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 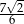 B)
B) 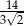 C)
C) 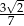 D)
D) 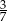
Objętość ostrosłupa prawidłowego czworokątnego jest równa 75, a pole jego podstawy jest równe 25. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 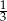 B)
B) 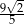 C)
C) 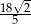 D)
D) 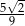
Liczba przekątnych o długości 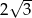 w sześciokącie foremnym o boku długości 2 jest równa
w sześciokącie foremnym o boku długości 2 jest równa
A) 0 B) 3 C) 6 D) 9

