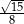Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 16 B) 20 C) 25 D) 30
/Szkoła średnia/Zadania testowe
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 17 B) 18 C) 19 D) 20
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są większe od 4 jest
A) 16 B) 20 C) 25 D) 30
Ze zbioru 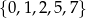 losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
A) 20 B) 16 C) 12 D) 10
Liczba 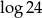 jest równa
jest równa
A) 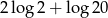 B)
B) 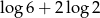 C)
C) 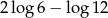 D)
D) 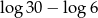
Liczba 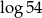 jest równa
jest równa
A) 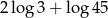 B)
B) 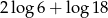 C)
C) 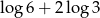 D)
D) 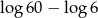
Liczba 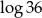 jest równa
jest równa
A) 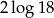 B)
B) 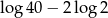 C)
C) 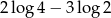 D)
D) 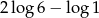
Liczba 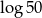 jest równa
jest równa
A) 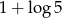 B)
B) 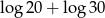 C)
C) 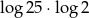 D)
D) 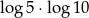
Liczba 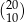 jest podzielna przez
jest podzielna przez
A) 5 B) 33 C) 221 D) 51
Liczba 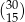 jest podzielna przez
jest podzielna przez
A) 7 B) 55 C) 143 D) 85
Objętość ostrosłupa prawidłowego czworokątnego jest równa 270, a pole jego podstawy jest równe 81. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 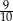 B)
B) 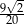 C)
C) 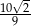 D)
D) 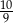
Objętość ostrosłupa prawidłowego czworokątnego jest równa 84, a pole jego podstawy jest równe 36. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 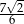 B)
B) 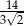 C)
C) 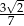 D)
D) 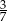
Objętość ostrosłupa prawidłowego czworokątnego jest równa 75, a pole jego podstawy jest równe 25. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 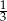 B)
B) 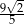 C)
C) 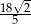 D)
D) 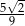
Liczba przekątnych o długości 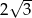 w sześciokącie foremnym o boku długości 2 jest równa
w sześciokącie foremnym o boku długości 2 jest równa
A) 0 B) 3 C) 6 D) 9
Wielomiany 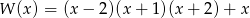 i
i 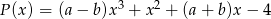 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 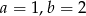 B)
B) 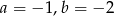 C)
C) 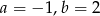 D)
D) 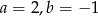
Wielomiany 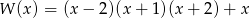 i
i 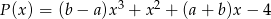 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 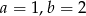 B)
B) 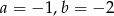 C)
C) 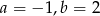 D)
D) 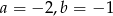
Wielomiany 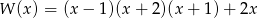 i
i 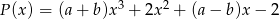 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 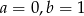 B)
B) 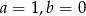 C)
C) 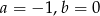 D)
D) 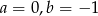
W prostokącie 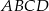 dane są
dane są 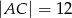 oraz
oraz 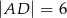 . Wówczas cosinus kąta
. Wówczas cosinus kąta 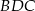 jest równy
jest równy
A) 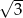 B)
B) 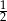 C)
C) 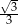 D)
D) 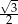
Okrąg jest styczny do boku 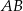 trójkąta
trójkąta 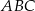 w punkcie
w punkcie 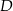 oraz przecina boki
oraz przecina boki 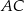 i
i 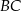 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 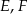 i
i 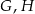 (zobacz rysunek). Kat
(zobacz rysunek). Kat 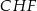 ma miarę
ma miarę 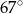 .
.
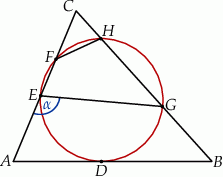
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 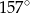 B)
B) 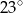 C)
C) 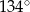 D)
D) 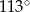
Okrąg jest styczny do boku 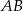 trójkąta
trójkąta 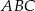 w punkcie
w punkcie 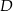 oraz przecina boki
oraz przecina boki 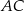 i
i 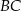 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 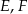 i
i 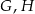 (zobacz rysunek). Kat
(zobacz rysunek). Kat 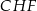 ma miarę
ma miarę 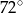 .
.
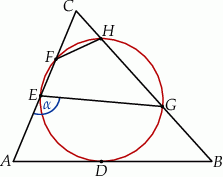
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 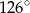 B)
B) 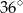 C)
C) 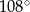 D)
D) 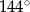
Prosta 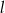 ma równanie
ma równanie 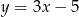 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 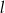 i przechodzącej przez punkt
i przechodzącej przez punkt 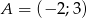 ma postać:
ma postać:
A) 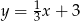 B)
B) 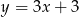 C)
C) 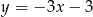 D)
D) 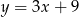
W kartezjańskim układzie współrzędnych 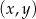 dana jest prosta
dana jest prosta 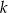 o równaniu
o równaniu 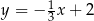 . Prosta o równaniu
. Prosta o równaniu 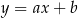 jest równoległa do prostej
jest równoległa do prostej 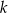 i przechodzi przez punkt
i przechodzi przez punkt 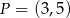 , gdy
, gdy
A) 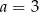 i
i 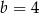 B)
B) 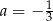 i
i 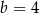 C)
C) 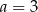 i
i 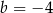 D)
D) 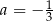 i
i 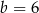
W kartezjańskim układzie współrzędnych 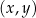 dana jest prosta
dana jest prosta 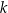 o równaniu
o równaniu 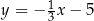 . Prosta o równaniu
. Prosta o równaniu 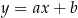 jest równoległa do prostej
jest równoległa do prostej 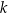 i przechodzi przez punkt
i przechodzi przez punkt 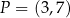 , gdy
, gdy
A) 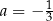 i
i 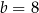 B)
B) 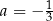 i
i 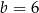 C)
C) 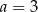 i
i 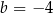 D)
D) 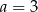 i
i 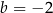
Prosta 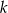 jest równoległa do prostej o równaniu
jest równoległa do prostej o równaniu 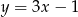 . Do wykresu prostej
. Do wykresu prostej 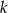 należy punkt
należy punkt 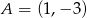 . Wskaż równanie prostej
. Wskaż równanie prostej 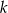 .
.
A) 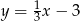 B)
B) 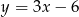 C)
C) 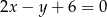 D)
D) 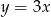
Równanie prostej równoległej do prostej 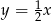 przechodzącej przez punkt
przechodzącej przez punkt 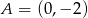 ma postać
ma postać
A) 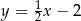 B)
B) 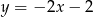 C)
C) 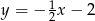 D)
D) 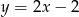
Dana jest prosta 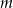 o równaniu
o równaniu 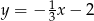 . Prosta
. Prosta 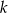 równoległa do prostej
równoległa do prostej 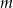 i przechodząca przez punkt
i przechodząca przez punkt 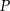 o współrzędnych
o współrzędnych 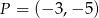 ma równanie
ma równanie
A) 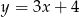 B)
B) 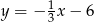 C)
C) 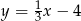 D)
D) 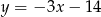
Prosta 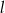 ma równanie
ma równanie 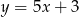 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 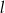 i przechodzącej przez punkt
i przechodzącej przez punkt 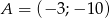 ma postać:
ma postać:
A) 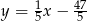 B)
B) 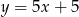 C)
C) 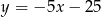 D)
D) 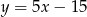
Prostą przechodzącą przez punkt 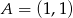 i równoległą do prostej
i równoległą do prostej 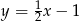 opisuje równanie
opisuje równanie
A) 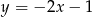 B)
B) 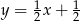 C)
C) 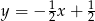 D)
D) 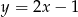
Prosta 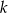 ma równanie
ma równanie 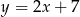 . Wskaż równanie prostej
. Wskaż równanie prostej 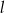 równoległej do prostej
równoległej do prostej 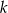 i przechodzącej przez punkt
i przechodzącej przez punkt 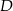 o współrzędnych
o współrzędnych 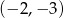 .
.
A) 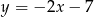 B)
B) 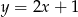 C)
C) 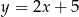 D)
D) 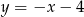
Dana jest prosta 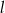 o równaniu
o równaniu 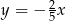 . Prosta
. Prosta 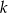 równoległa do prostej
równoległa do prostej 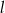 i przecinająca oś
i przecinająca oś 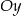 w punkcie o współrzędnych
w punkcie o współrzędnych 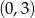 ma równanie
ma równanie
A) 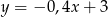 B)
B) 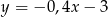 C)
C) 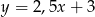 D)
D) 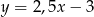
Równanie prostej przechodzącej przez punkt 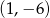 i równoległej do prostej
i równoległej do prostej 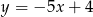 jest dane wzorem
jest dane wzorem
A) 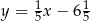 B)
B) 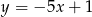 C)
C) 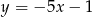 D)
D) 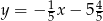
Prosta 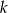 ma równanie
ma równanie 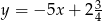 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 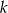 , przechodzącej przez punkt
, przechodzącej przez punkt 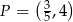 .
.
A) 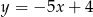 B)
B) 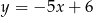 C)
C) 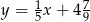 D)
D) 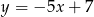
W kartezjańskim układzie współrzędnych 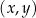 dane są prosta
dane są prosta 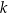 o równaniu
o równaniu 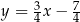 oraz punkt
oraz punkt 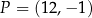 . Prosta przechodząca przez punkt
. Prosta przechodząca przez punkt 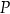 i równoległa do prostej
i równoległa do prostej 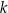 ma równanie
ma równanie
A) 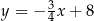 B)
B) 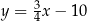 C)
C) 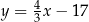 D)
D) 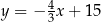
Prosta 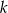 ma równanie
ma równanie 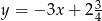 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 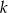 , przechodzącej przez punkt
, przechodzącej przez punkt 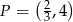 .
.
A) 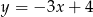 B)
B) 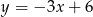 C)
C) 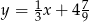 D)
D) 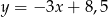
Prosta 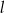 jest równoległa do prostej
jest równoległa do prostej 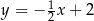 . Na prostej
. Na prostej 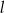 leży punkt
leży punkt 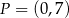 . Zatem równanie prostej
. Zatem równanie prostej 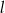 ma postać
ma postać
A) 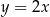 B)
B) 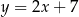 C)
C) 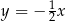 D)
D) 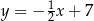
Prosta 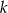 ma równanie
ma równanie 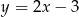 . Wskaż równanie prostej
. Wskaż równanie prostej 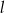 równoległej do prostej
równoległej do prostej 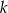 i przechodzącej przez punkt
i przechodzącej przez punkt 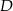 o współrzędnych
o współrzędnych 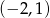 .
.
A) 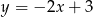 B)
B) 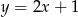 C)
C) 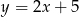 D)
D) 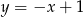
Prosta 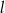 jest równoległa do prostej
jest równoległa do prostej 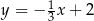 . Na prostej
. Na prostej 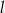 leży punkt
leży punkt 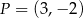 . Zatem równanie prostej
. Zatem równanie prostej 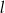 ma postać
ma postać
A) 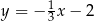 B)
B) 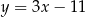 C)
C) 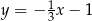 D)
D) 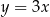
Wartość wyrażenia 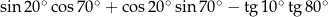 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Wartość wyrażenia 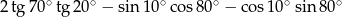 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Wartość wyrażenia 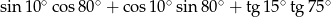 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Prosta przechodząca przez punkt 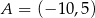 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 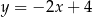 B)
B) 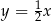 C)
C) 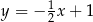 D)
D) 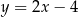
Prosta przechodząca przez punkt 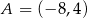 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 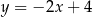 B)
B) 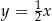 C)
C) 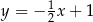 D)
D) 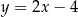
Prosta przechodząca przez punkt 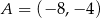 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 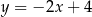 B)
B) 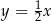 C)
C) 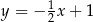 D)
D) 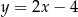
Dana jest funkcja 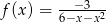 . Wskaż maksymalny zbiór, na którym funkcja
. Wskaż maksymalny zbiór, na którym funkcja 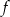 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
A) 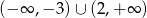 B)
B) 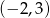 C)
C) 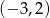 D)
D) 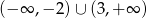
Punkty 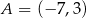 i
i 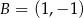 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 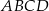 . Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
. Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
A) 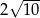 B)
B) 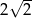 C)
C) 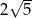 D)
D) 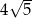
Najmniejszą liczbą naturalną, która nie spełnia nierówności 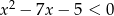 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą naturalną, która nie spełnia nierówności 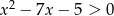 jest
jest
A) 0 B) 3 C) 7 D) 8
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
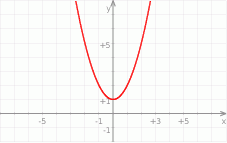
A) 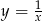 B)
B) 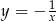 C)
C) 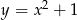 D)
D) 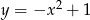
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
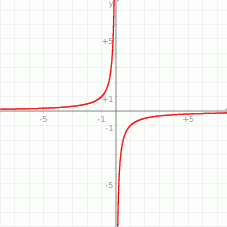
A) 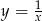 B)
B) 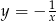 C)
C) 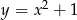 D)
D) 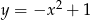
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
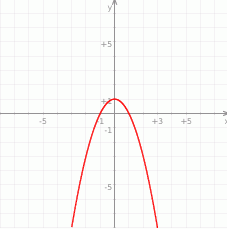
A) 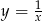 B)
B) 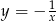 C)
C) 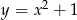 D)
D) 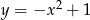
Liczba 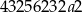 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 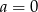 B)
B) 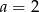 C)
C) 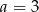 D)
D) 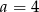
W liczbie pięciocyfrowej 258#4, podzielnej przez 4 i niepodzielnej przez 3, cyfrę dziesiątek zastąpiono znakiem „#”. Jakiej cyfry na pewno nie zastąpiono znakiem „#”?
A) 0 B) 4 C) 6 D) 8
Liczba 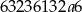 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 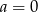 B)
B) 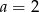 C)
C) 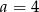 D)
D) 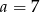
Dane są okręgi styczne wewnętrznie o środkach 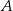 i
i 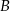 . Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i
. Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i 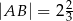 . Promienie tych okręgów mają długość
. Promienie tych okręgów mają długość
A) 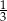 i 3 B)
i 3 B) 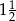 i
i 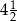 C)
C)  i 2 D)
i 2 D) 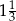 i 4
i 4
Czas trwania zabiegu rehabilitacyjnego wydłużono o 35% do 108 minut. Ile początkowo miał trwać ten zabieg?
A) 80 minut B) 90 minut C) 60 minut D) 70 minut
Piotrek ma w swojej bibliotece tylko książki historyczne i biograficzne. Książek historycznych ma 9, co stanowi 30% wszystkich jego książek. Wynika stąd, że liczba książek biograficznych Piotrka, to
A) 21 B) 30 C) 16 D) 10
Karol ma w swojej bibliotece tylko książki przyrodnicze i sensacyjne. Książek przyrodniczych ma 12, co stanowi 40% wszystkich jego książek. Wynika stąd, że liczba książek sensacyjnych Karola, to
A) 21 B) 18 C) 36 D) 24
Gienek ma w swojej bibliotece tylko książki przygodowe i historyczne. Książek historycznych ma 21, co stanowi 35% wszystkich jego książek. Wynika stąd, że liczba książek przygodowych Gienka, to
A) 21 B) 31 C) 39 D) 43
Dany jest trójkąt prostokątny 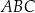 , w którym
, w którym 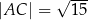 i
i 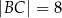 . Na przyprostokątnej
. Na przyprostokątnej 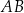 leży taki punkt
leży taki punkt 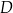 , że
, że 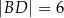 (zobacz rysunek).
(zobacz rysunek).

Tangens kąta ostrego
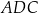 jest równy
jest równy A)
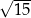 B)
B)  C)
C) 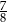 D)
D)