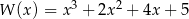Na rysunku przedstawiono fragment wykresu pochodnej 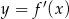 funkcji
funkcji 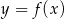 .
.
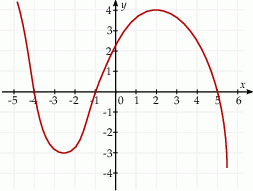
Funkcja 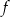 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 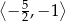 B)
B) 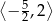 C)
C) 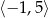 D)
D) 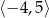
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment wykresu pochodnej 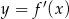 funkcji
funkcji 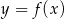 .
.

Funkcja 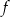 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 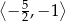 B)
B) 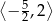 C)
C) 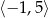 D)
D) 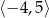
Na rysunku przedstawiono fragment wykresu pochodnej 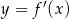 funkcji
funkcji 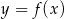 .
.
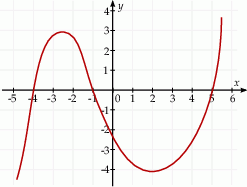
Funkcja 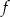 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 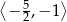 B)
B) 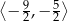 C)
C) 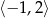 D)
D) 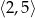
Na rysunku przedstawiono fragment wykresu pochodnej 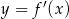 funkcji
funkcji 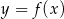 .
.
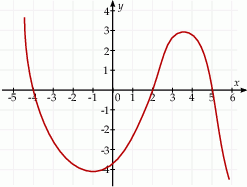
Funkcja 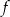 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 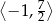 B)
B) 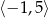 C)
C) 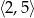 D)
D) 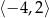
Na rysunku przedstawiono fragment wykresu pochodnej 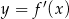 funkcji
funkcji 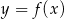 .
.
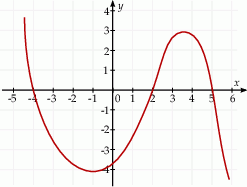
Funkcja 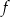 jest malejąca w przedziale
jest malejąca w przedziale
A) 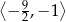 B)
B) 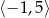 C)
C) 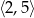 D)
D) 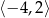
Na rysunku przedstawiono fragment wykresu pochodnej 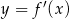 funkcji
funkcji 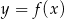 .
.
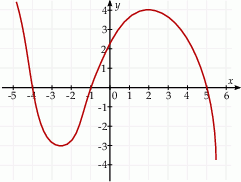
Funkcja 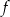 jest malejąca w przedziale
jest malejąca w przedziale
A) 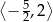 B)
B) 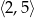 C)
C) 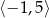 D)
D) 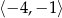
Na rysunku przedstawiono fragment wykresu pochodnej 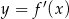 funkcji
funkcji 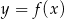 .
.
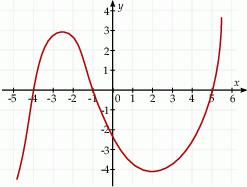
Funkcja 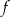 jest malejąca w przedziale
jest malejąca w przedziale
A) 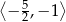 B)
B) 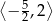 C)
C) 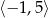 D)
D) 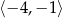
Wskaż rysunek, na którym przedstawiono fragment wykresu funkcji
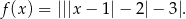
Na rysunku przedstawiony jest czworościan foremny  . Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą:
. Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą:
A)  B)
B) 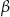 C)
C) 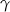 D)
D) 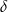
Na rysunku przedstawiony jest ostrosłup prawidłowy trójkątny 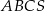 . Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
. Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
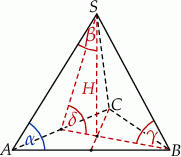
A)  B)
B)  C)
C)  D)
D) 
Na którym rysunku przedstawiono wykres funkcji liniowej 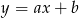 takiej, że
takiej, że 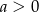 i
i 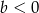 ?
?
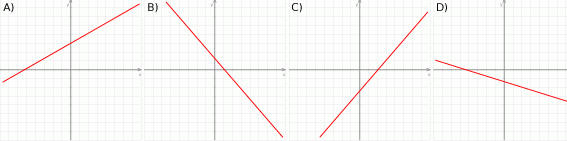
Na którym rysunku przedstawiono wykres funkcji liniowej 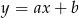 takiej, że
takiej, że 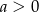 i
i 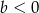 ?
?
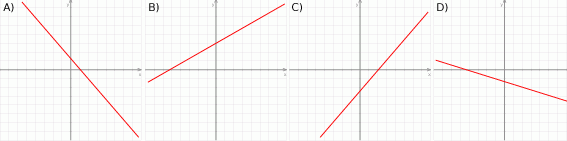
Na którym rysunku przedstawiono wykres funkcji liniowej 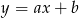 takiej, że
takiej, że 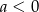 i
i 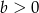 ?
?
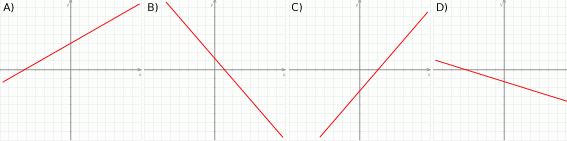
Na którym rysunku przedstawiono wykres funkcji liniowej 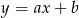 takiej, że
takiej, że 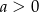 i
i 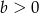 ?
?
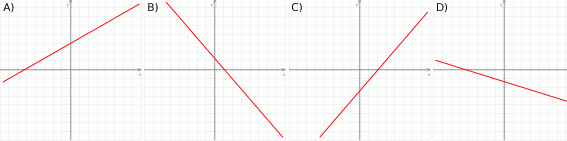
Na którym rysunku przedstawiono wykres funkcji liniowej 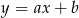 takiej, że
takiej, że 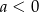 i
i 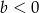 ?
?
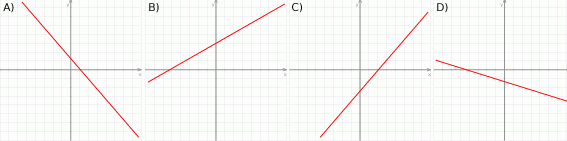
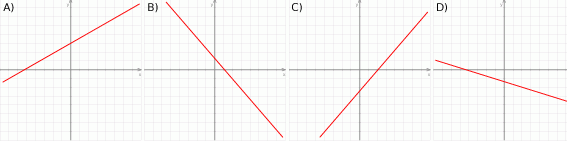
Na którym rysunku przedstawiono wykres funkcji liniowej 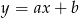 takiej, że
takiej, że 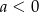 i
i 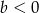 ?
?
Obwód trójkąta prostokątnego równoramiennego wynosi 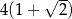 . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
. Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 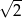 B) 4 C) 2 D)
B) 4 C) 2 D) 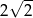
Ciągi 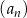 ,
, 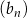 oraz
oraz 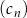 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 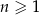 następująco:
następująco:
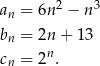
Wskaż zdanie prawdziwe.
A) Ciąg 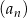 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 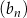 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 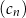 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 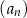 ,
, 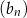 ,
, 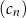 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Ciągi 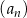 ,
, 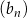 oraz
oraz 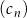 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 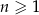 następująco:
następująco:
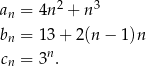
Wskaż zdanie prawdziwe.
A) Ciąg 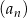 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 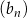 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 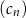 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 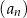 ,
, 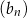 ,
, 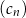 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Wykres funkcji 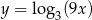 powstaje z przesunięcia wykresu funkcji
powstaje z przesunięcia wykresu funkcji 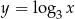
A) o 2 jednostki w dół B) o 2 jednostki w górę
C) o 2 jednostki w prawo D) o 2 jednostki w lewo
Wykres funkcji 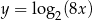 powstaje z przesunięcia wykresu funkcji
powstaje z przesunięcia wykresu funkcji 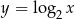
A) o 8 jednostek w górę B) o 8 jednostki w dół
C) o 3 jednostki w dół D) o 3 jednostki w górę
Wykres funkcji 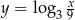 powstaje z przesunięcia wykresu funkcji
powstaje z przesunięcia wykresu funkcji 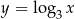
A) o 2 jednostki w dół B) o 2 jednostki w górę
C) o 2 jednostki w prawo D) o 2 jednostki w lewo
Samochód pokonał trasę długości 117 km w ciągu 39 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 141 km, to zajęłoby to
A) 47 minut. B) 45 minut. C) 48 minut. D) 44 minuty.
Samochód pokonał trasę długości 115 km w ciągu 46 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 240 km, to zajęłoby to
A) 94 minuty. B) 90 minut. C) 96 minut. D) 88 minut.
Stopień wielomianu 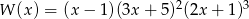 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Stopień wielomianu 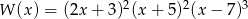 jest równy
jest równy
A) 4 B) 5 C) 6 D) 7
Stopień wielomianu 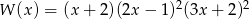 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Równanie 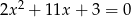
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Równanie 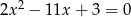
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 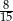 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 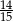 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
A) 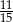 B)
B) 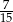 C)
C) 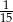 D)
D) 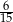
Z pudełka zwierającego losy wygrywające i przegrywające wybieramy dwa losy. Prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego jest równe 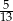 , a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe
, a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe 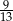 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
A) 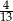 B)
B) 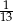 C)
C) 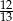 D)
D) 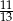
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej jest równe 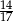 , a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe 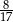 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
A) 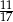 B)
B) 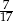 C)
C) 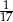 D)
D) 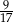
Pani Weronika wpłaciła do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 4% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania kapitał zgromadzony na lokacie (bez uwzględnienia podatków) był o 270,40 zł większy od kapitału zgromadzonego po roku oszczędzania. Kwota wpłacona przez panią Weronikę na tę lokatę była równa
A) 5800 zł B) 6500 zł C) 6400 zł D) 4800 zł
Dwa kolejne wyrazy ciągu arytmetycznego są równe 79 i 75. Wyrazem tego ciągu może być liczba
A) 2015 B) 2016 C) 2017 D) 2018
Liczba 1,1 jest przybliżeniem z niedomiarem liczby 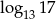 i błąd bezwzględny tego przybliżenia jest mniejszy od 0,01. Liczba
i błąd bezwzględny tego przybliżenia jest mniejszy od 0,01. Liczba
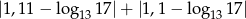
jest równa
A) 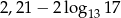 B) 0,01 C)
B) 0,01 C) 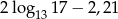 D) 2,21
D) 2,21
Zbiorem wartości funkcji  , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
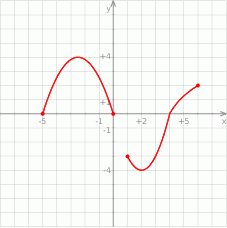
A) 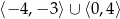 B)
B) 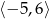 C)
C) 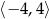 D)
D) 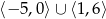
Na rysunku przedstawiono wykres funkcji 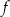 .
.
Zbiorem wartości funkcji  jest zbiór
jest zbiór
A)  B)
B) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/9110159/HzadT4x.png)
C) 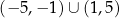 D)
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/9110159/HzadT6x.png)
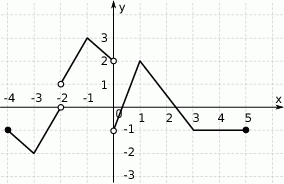
Na rysunku przedstawiono wykres funkcji f(x). Zbiorem wartości tej funkcji jest:
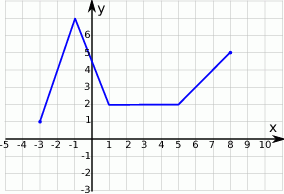
A) 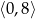 B)
B) 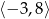 C)
C) 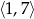 D)
D) 
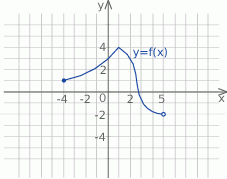
Na rysunku przedstawiono wykres funkcji  .
.
Zbiorem wartości funkcji 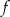 jest
jest
A) 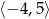 B)
B) 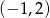 C)
C) 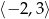 D)
D) 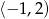
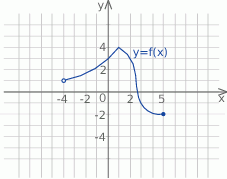
Dany jest wykres funkcji 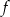 . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 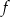 jest przedział
jest przedział
A) 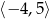 B)
B) 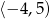 C)
C) 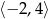 D)
D) 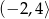
Dany jest wykres funkcji 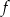 . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 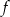 jest przedział
jest przedział
A) 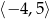 B)
B) 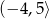 C)
C) 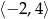 D)
D) 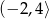
Na rysunku przedstawiono wykres funkcji 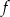 .
.
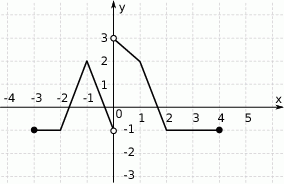
Zbiorem wartości funkcji  jest przedział
jest przedział
A)  B)
B)  C)
C) 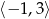 D)
D) 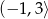
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest
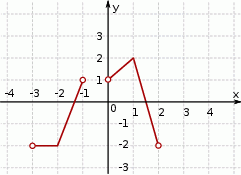
A) 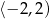 B)
B) 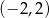 C)
C) 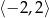 D)
D) 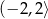
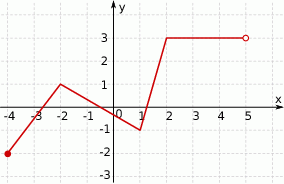
Na rysunku przedstawiono wykres funkcji 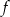 .
.
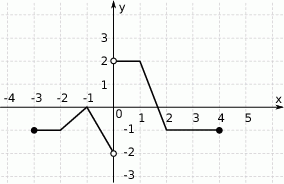
Zbiorem wartości funkcji  jest
jest
A)  B)
B)  C)
C) 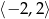 D)
D) 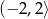
Zbiorem wartości funkcji, której wykres jest przedstawiony na rysunku jest przedział
A) 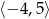 B)
B) 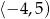 C)
C) 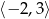 D)
D) 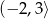
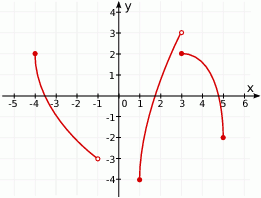
Na rysunku jest przedstawiony wykres funkcji 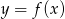 .
.
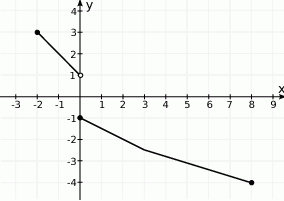
Zbiorem wartości tej funkcji jest
A) 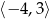 B)
B) 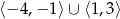 C)
C) 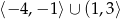 D)
D) 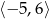
Zbiorem wartości funkcji 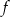 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
A) 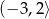 B)
B) 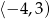 C)
C) 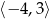 D)
D) 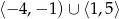
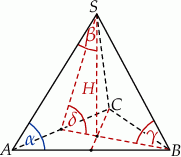
Dany jest trapez równoramienny 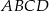 o podstawach
o podstawach 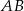 i
i 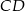 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 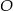 . Jeśli
. Jeśli 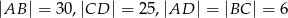 , to
, to
A) 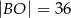 B)
B) 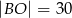 C)
C) 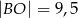 D)
D) 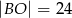
Dany jest trapez równoramienny o podstawach 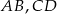 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie  . Jeśli
. Jeśli 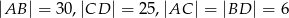 , to
, to
A)  B)
B) 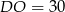 C)
C) 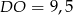 D)
D) 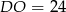
Dany jest trapez równoramienny o podstawach 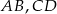 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie  . Jeśli
. Jeśli 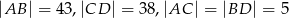 , to
, to
A) 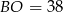 B)
B) 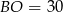 C)
C) 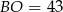 D)
D) 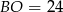
Suma miar kąta wpisanego i kąta środkowego, opartych na 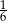 okręgu, jest równa
okręgu, jest równa
A) 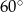 B)
B) 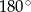 C)
C) 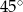 D)
D) 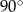
Równanie 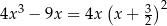 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Równanie 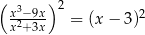
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Wśród miejsc zerowych wielomianu są liczby 0, 1, 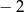 . Wielomian może mieć postać:
. Wielomian może mieć postać:
A) 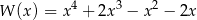 B)
B) 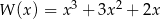
C) 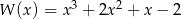 D)
D)