Jeżeli 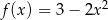 to funkcja
to funkcja 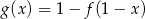 ma wzór
ma wzór
A) 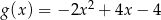 B)
B) 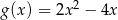
C) 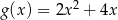 D)
D) 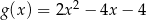
/Szkoła średnia/Zadania testowe
Jeżeli funkcja 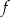 jest określona wzorem
jest określona wzorem 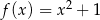 , to funkcję
, to funkcję 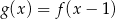 opisuje wzór
opisuje wzór
A) 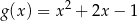 B)
B) 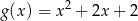
C) 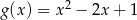 D)
D) 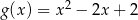
W trójkącie równoramiennym 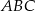 dane są
dane są 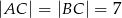 oraz
oraz 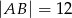 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 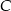 jest równa
jest równa
A) 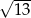 B)
B) 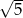 C) 1 D) 5
C) 1 D) 5
W trójkącie równoramiennym 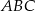 dane są
dane są 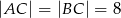 oraz
oraz 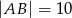 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 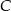 jest równa
jest równa
A) 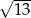 B)
B) 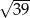 C) 6 D)
C) 6 D) 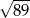
W trójkącie równoramiennym 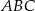 dane są
dane są 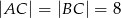 oraz
oraz 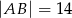 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 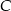 jest równa
jest równa
A) 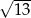 B)
B) 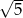 C)
C) 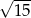 D)
D) 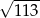
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 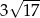 B)
B) 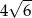 C)
C) 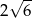 D)
D) 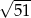
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 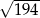 B)
B) 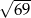 C) 12 D) 11
C) 12 D) 11
W trójkącie równoramiennym 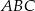 dane są
dane są 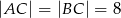 oraz
oraz 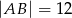 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 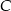 jest równa
jest równa
A) 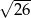 B)
B) 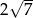 C) 2 D)
C) 2 D) 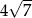
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 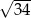 D)
D) 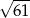
Odcinek 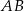 jest średnicą okręgu o środku
jest średnicą okręgu o środku 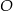 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 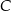 , taki, że
, taki, że 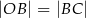 (zobacz rysunek).
(zobacz rysunek).
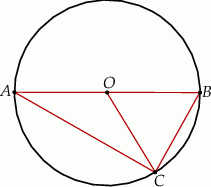
Pole trójkąta 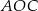 jest równe
jest równe
A) 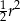 B)
B) 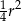 C)
C) 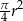 D)
D) 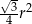
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 10 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 5,9 m. Ile trójkątów przedstawia mural?
A) 49 B) 50 C) 59 D) 60
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 15 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 6,4 m. Ile trójkątów przedstawia mural?
A) 35 B) 36 C) 37 D) 40
Wartość wyrażenia 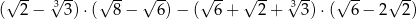 jest równa
jest równa
A) 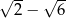 B) 2 C)
B) 2 C) 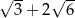 D)
D) 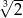
Iloczyn 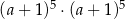 jest równy
jest równy
A) 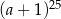 B)
B) 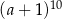 C)
C) 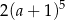 D)
D) 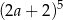
Na rysunkach A–F w kartezjańskim układzie współrzędnych 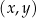 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 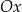 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 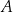 lub
lub 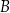 , lub
, lub 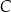 , lub
, lub 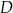 , lub
, lub 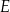 , lub
, lub 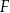 .
.
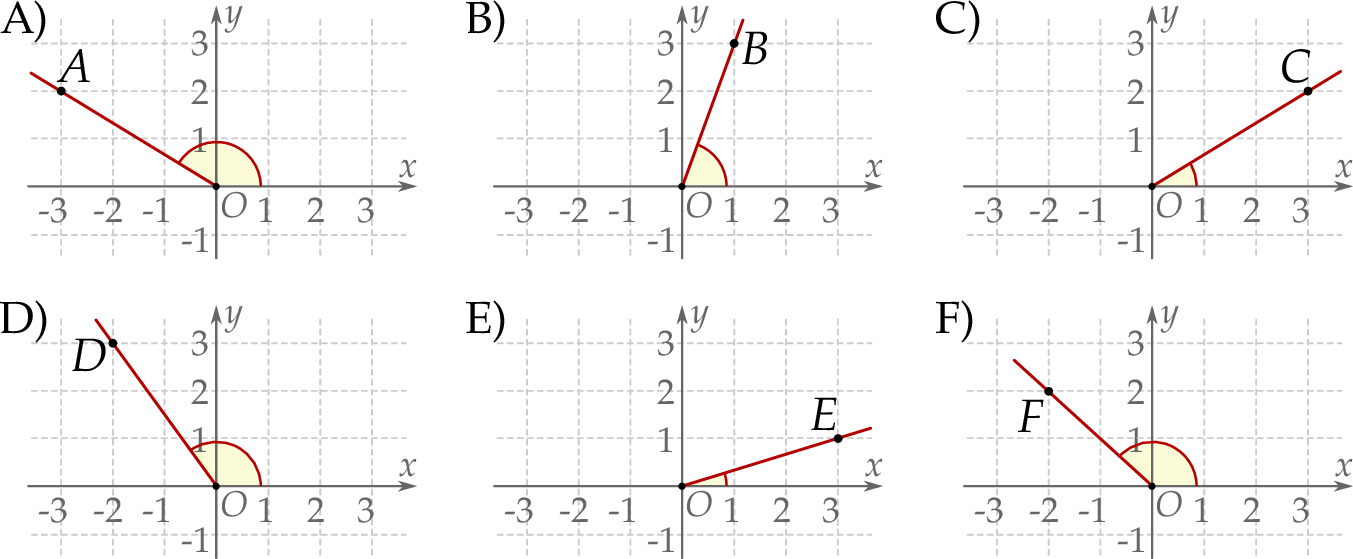
Na którym z rysunków zaznaczono kąt 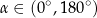 , spełniający warunek
, spełniający warunek 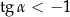 ?
?
Na rysunkach A–F w kartezjańskim układzie współrzędnych 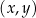 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 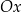 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 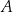 lub
lub 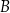 , lub
, lub 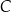 , lub
, lub 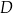 , lub
, lub 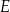 , lub
, lub 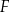 .
.
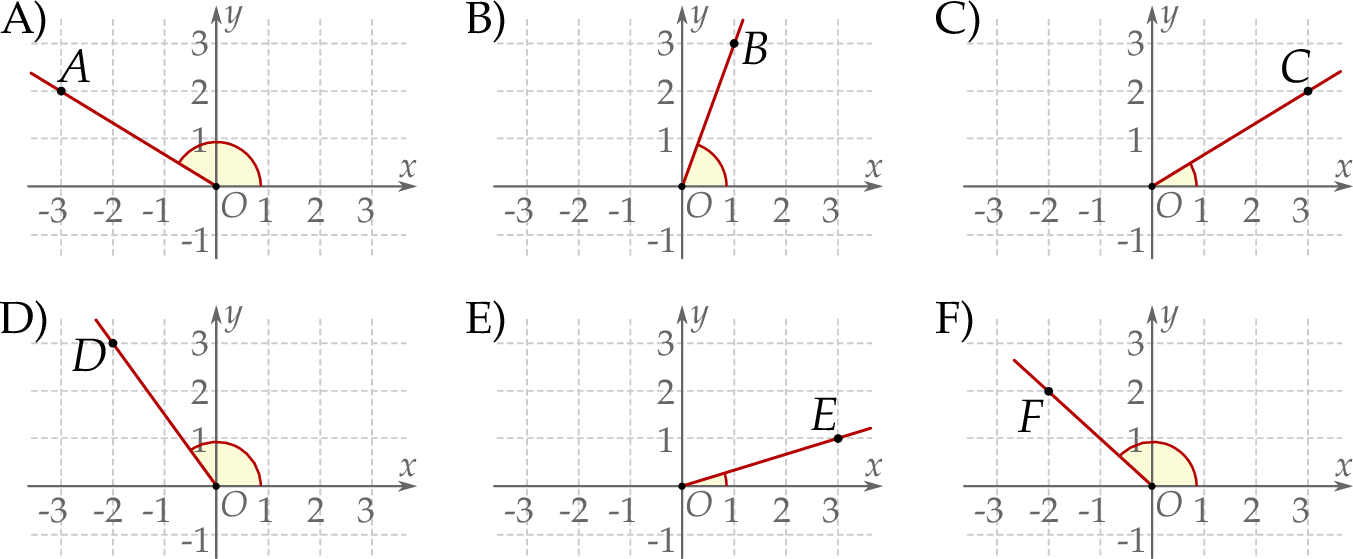
Na którym z rysunków zaznaczono kąt 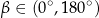 , spełniający warunek
, spełniający warunek 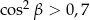 ?
?
Najmniejszą liczbą  spełniającą nierówność
spełniającą nierówność
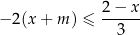
jest 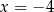 . Liczba
. Liczba 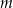 jest więc równa
jest więc równa
A) 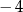 B)
B) 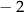 C) 4 D) 3
C) 4 D) 3
Punkt 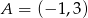 należy do wykresu funkcji
należy do wykresu funkcji 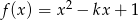 . Zatem
. Zatem 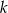 jest równe
jest równe
A) 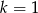 B)
B) 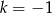 C)
C) 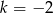 D)
D) 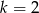
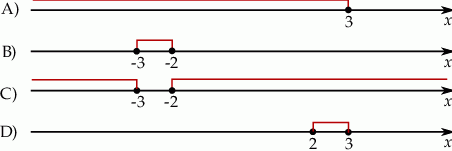
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 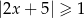 .
.
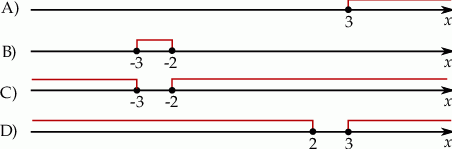
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 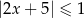 .
.
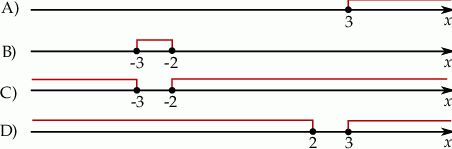
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 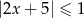 .
.
Dany jest wielomian 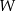 określony wzorem
określony wzorem 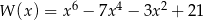 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 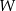 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 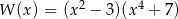 B)
B) 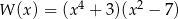
C) 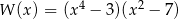 D)
D) 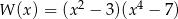
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 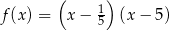 B)
B) 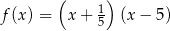
C) 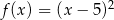 D)
D) 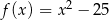
Pierwiastki trójmianu kwadratowego są liczbami odwrotnymi. Te warunki spełnia trójmian
A) 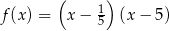 B)
B) 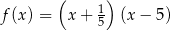
C) 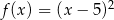 D)
D) 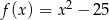
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 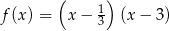 B)
B) 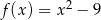
C) 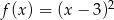 D)
D) 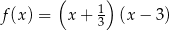
Pole prostokąta przedstawionego na rysunku jest równe 20. Zatem

A) 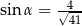 B)
B) 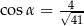 C)
C) 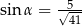 D)
D) 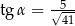
Pole prostokąta przedstawionego na rysunku jest równe 18. Zatem
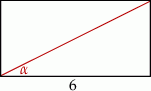
A) 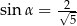 B)
B) 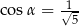 C)
C) 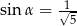 D)
D) 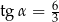
Na prostej 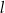 o współczynniku kierunkowym
o współczynniku kierunkowym 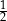 leżą punkty
leżą punkty 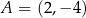 oraz
oraz 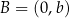 . Wtedy liczba
. Wtedy liczba 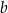 jest równa
jest równa
A) 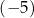 B) 10 C)
B) 10 C) 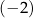 D) 0
D) 0
Objętość walca o wysokości 8 jest równa 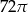 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Objętość walca o wysokości 4 jest równa 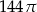 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Rysunek przedstawia wykres funkcji 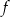 .
.
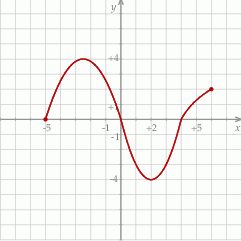
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 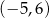 B)
B) 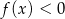 dla
dla 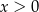
C) funkcja ma dwa miejsca zerowe D) zbiór wartości funkcji to 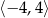
Na rysunku przedstawiono wykres funkcji 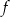 określonej w zbiorze
określonej w zbiorze 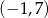 .
.
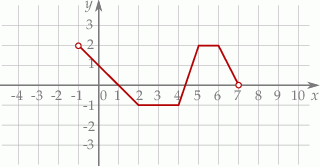
Wskaż zdanie prawdziwe.
A) Funkcja 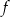 ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 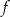 jest
jest 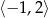 .
.
C) Funkcja 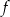 nie przyjmuje wartości 2.
nie przyjmuje wartości 2.
D) Funkcja 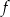 osiąga wartości dodatnie dla argumentów ze zbioru
osiąga wartości dodatnie dla argumentów ze zbioru 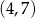 .
.
Na rysunku przedstawiono wykres funkcji 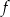 określonej w zbiorze
określonej w zbiorze 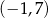 .
.
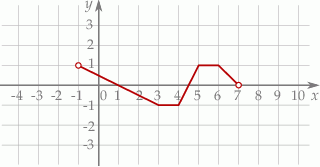
Wskaż zdanie prawdziwe.
A) Funkcja 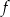 ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 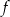 jest
jest 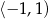 .
.
C) Funkcja 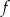 osiąga wartość największą równą 1.
osiąga wartość największą równą 1.
D) Funkcja 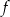 osiąga wartości ujemne dla argumentów ze zbioru
osiąga wartości ujemne dla argumentów ze zbioru 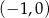 .
.
Na wykresie przedstawiono wykres funkcji 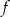 .
.
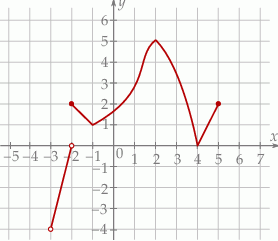
Wskaż zdanie prawdziwe.
A) Dziedziną funkcji 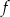 jest przedział
jest przedział 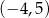 .
.
B) Funkcja 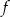 ma dwa miejsca zerowe.
ma dwa miejsca zerowe.
C) Funkcja 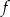 dla argumentu 1 przyjmuje wartość
dla argumentu 1 przyjmuje wartość 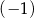 .
.
D) Zbiorem wartości funkcji 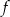 jest przedział
jest przedział ![(− 4,5]](https://img.zadania.info/zad/3523914/HzadT8x.gif) .
.
Rysunek przedstawia wykres funkcji 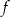 .
.
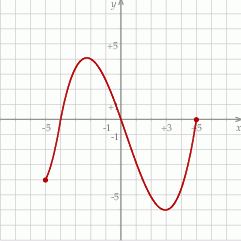
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 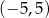 B)
B) 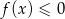 dla
dla 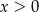
C) funkcja ma dwa miejsca zerowe D) zbiór wartości funkcji to 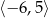
Rysunek przedstawia wykres funkcji 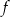 .
.
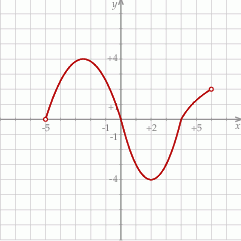
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 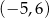 B)
B) 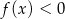 dla
dla 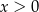
C) funkcja ma trzy miejsca zerowe D) zbiór wartości funkcji to 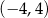
Liczba 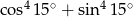 jest równa
jest równa
A) 1 B)  C)
C) 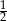 D)
D) 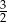
Dane są dwa okręgi o promieniach 8 i 13. Okręgi te są styczne wewnętrznie, gdy odległość ich środków jest równa
A) 8 B) 21 C) 5 D) 13
Dane są dwa okręgi styczne zewnętrznie o promieniach 4 i 10. Odległość między środkami tych okręgów jest równa
A) 6 B) 8 C) 14 D) 10
Dane są dwa okręgi styczne wewnętrznie o promieniach 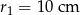 i
i 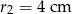 . Zatem odległość między ich środkami jest równa
. Zatem odległość między ich środkami jest równa
A) 2 cm B) 6 cm C) 8 cm D) 14 cm
Dane są dwa okręgi styczne zewnętrznie o promieniach 6 i 13. Odległość między środkami tych okręgów jest równa
A) 7 B) 19 C) 13 D) 10
Dane są dwa okręgi o promieniach 27 i 11. Okręgi te są styczne wewnętrznie, gdy odległość między ich środkami jest równa
A) 38 B) 27 C) 16 D) 11
Jeżeli do zestawu czterech danych: 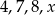 dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 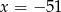 B)
B) 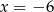 C)
C) 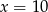 D)
D) 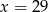
Jeżeli do zestawu czterech danych: 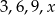 dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 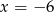 B)
B) 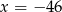 C)
C) 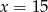 D)
D) 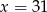
Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
A) 0 B) 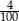 C) 3,57 D) 4
C) 3,57 D) 4
Gdy do 50% liczby 73 dodamy 73% liczby 50, to otrzymamy
A) 1 B) 73 C) 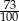 D) 100
D) 100
Gdy od 19% liczby 32 odejmiemy 16% liczby 19, to otrzymamy
A) 0 B) 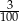 C) 3,04 D) 9,12
C) 3,04 D) 9,12

