Na ile sposobów można włożyć dwie skarpetki do czterech szuflad?
A) 16 B) 8 C) 256 D) 32
/Szkoła średnia/Zadania testowe
Na ile sposobów można włożyć trzy skarpetki do czterech różnych szuflad?
A) 12 B) 81 C) 256 D) 64
Na ile sposobów można włożyć dwie czapki do pięciu różnych szuflad?
A) 10 B) 25 C) 64 D) 32
Funkcja 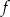 przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 5. Wówczas
przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 5. Wówczas 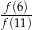 równa się
równa się
A) 1 B) 2 C) 3 D) 4
Średnie zużycie paliwa na pierwszym odcinku trasy było równe 7 litrów na 100 kilometrów, a średnie zużycie paliwa na drugim, dwa razy dłuższym odcinku trasy, było równe 10 litrów na 100 kilometrów. Średnie zużycie paliwa na każde 100 km całej trasy wyniosło
A) 8 litrów. B) 8,5 litra. C) 7 litrów. D) 9 litrów.
Dany jest okrąg o równaniu 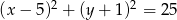 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 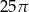 B)
B) 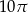 C)
C) 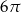 D)
D) 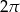
Dany jest okrąg o równaniu 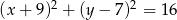 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 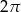 B)
B) 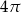 C)
C) 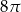 D)
D) 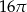
Dany jest okrąg o równaniu 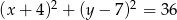 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 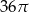 B)
B) 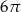 C)
C) 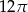 D)
D) 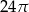
Funkcja 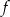 jest określona wzorem
jest określona wzorem 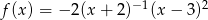 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 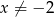 . Wartość funkcji
. Wartość funkcji 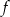 dla argumentu 2 jest równa
dla argumentu 2 jest równa
A) 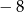 B)
B) 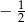 C)
C) 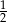 D) 8
D) 8
Funkcja 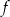 jest określona wzorem
jest określona wzorem 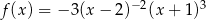 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 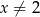 . Wartość funkcji
. Wartość funkcji 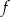 dla argumentu
dla argumentu 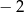 jest równa
jest równa
A) 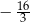 B)
B) 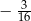 C)
C) 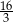 D)
D) 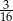
Liczby 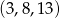 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 48 B) 103 C) 168 D) 190
Liczby 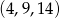 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 49 B) 191 C) 169 D) 104
Liczby 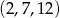 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 47 B) 112 C) 179 D) 147
W ostrosłupie prawidłowym czworokątnym 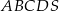 wszystkie krawędzie mają jednakową długość.
wszystkie krawędzie mają jednakową długość.
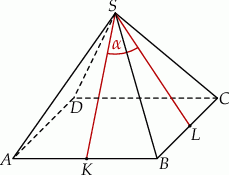
Oblicz cosinus kąta utworzonego przez wysokości 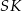 i
i 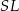 dwóch sąsiednich ścian bocznych.
dwóch sąsiednich ścian bocznych.
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 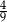 D)
D) 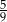
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 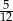 C)
C) 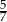 D) 0,4
D) 0,4
Wiadomo, że 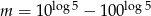 i
i 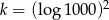 . Zatem
. Zatem
A) 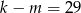 B)
B) 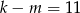 C)
C) 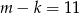 D)
D) 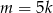
Wiadomo, że 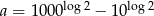 i
i 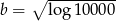 . Zatem
. Zatem
A) 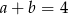 B)
B) 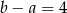 C)
C) 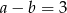 D)
D) 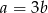
Wiadomo, że 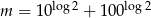 i
i 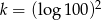 . Zatem
. Zatem
A) 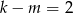 B)
B) 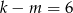 C)
C) 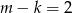 D)
D) 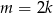
Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa 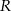 .
.
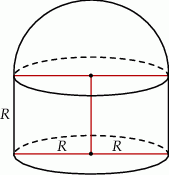
Objętość tej bryły jest równa
A) 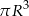 B)
B) 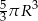 C)
C) 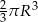 D)
D) 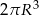
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
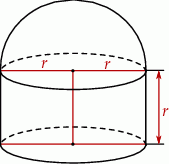
Objętość tej bryły jest równa
A) 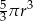 B)
B) 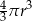 C)
C) 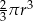 D)
D) 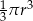
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
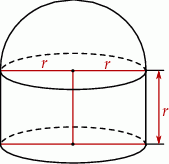
Pole powierzchni całkowitej tej bryły jest równe
A) 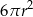 B)
B) 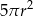 C)
C) 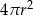 D)
D) 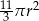
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest wygrywający, jest równe
A) 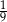 B)
B) 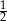 C)
C) 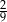 D)
D) 
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest przegrywający, jest równe
A) 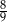 B)
B) 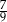 C)
C) 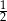 D)
D) 
Kąt między cięciwą 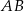 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 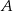 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 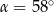 . Wówczas
. Wówczas
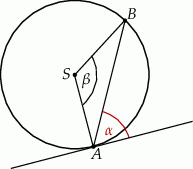
A) 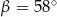 B)
B) 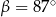 C)
C) 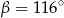 D)
D) 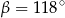
Punkty 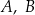 oraz
oraz 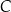 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 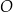 . Prosta
. Prosta 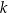 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 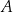 i tworzy z cięciwą
i tworzy z cięciwą 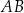 kąt o mierze
kąt o mierze 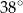 . Ponadto odcinek
. Ponadto odcinek 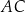 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 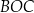 jest równa
jest równa
A) 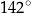 B)
B) 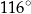 C)
C) 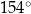 D)
D) 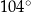
Kąt między cięciwą 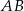 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 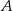 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 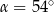 . Wówczas
. Wówczas
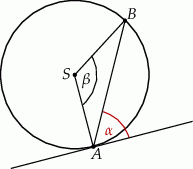
A) 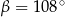 B)
B) 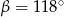 C)
C) 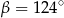 D)
D) 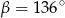
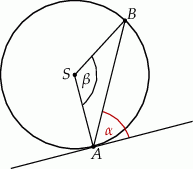
Kąt między cięciwą 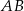 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 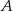 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 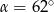 . Wówczas
. Wówczas
A) 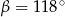 B)
B) 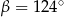 C)
C) 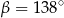 D)
D) 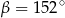
Punkty 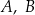 oraz
oraz 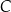 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 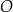 . Prosta
. Prosta 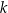 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 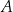 i tworzy z cięciwą
i tworzy z cięciwą 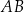 kąt o mierze
kąt o mierze 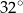 . Ponadto odcinek
. Ponadto odcinek 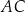 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 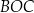 jest równa
jest równa
A) 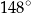 B)
B) 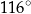 C)
C) 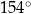 D)
D) 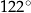
Suma trzech pierwszych wyrazów malejącego ciągu geometrycznego jest równa 10,5. Drugi wyraz tego ciągu jest równy 3. Czwarty wyraz tego ciągu jest równy
A) 1,5 B) 3,5 C) 0,75 D) 2,25
Liczba ujemnych pierwiastków równania 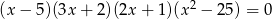 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 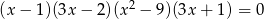 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 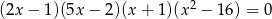 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 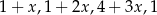 , jest równa 10. Wtedy
, jest równa 10. Wtedy
A) 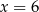 B)
B) 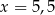 C)
C) 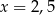 D)
D) 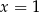
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 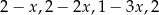 , jest równa
, jest równa 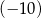 . Wtedy
. Wtedy
A) 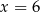 B)
B) 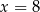 C)
C) 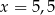 D)
D) 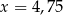
Liczba 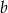 jest 3 razy większa od liczby
jest 3 razy większa od liczby  . Wtedy
. Wtedy
A) 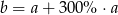 B)
B) 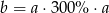 C)
C) 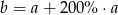 D)
D) 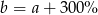
Liczba 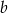 jest 2 razy większa od liczby
jest 2 razy większa od liczby  . Wtedy
. Wtedy
A) 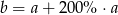 B)
B) 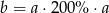 C)
C) 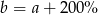 D)
D) 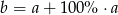
Podstawy trapezu równoramiennego 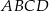 mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).
mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).

Wtedy miara  kąta ostrego
kąta ostrego 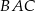 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 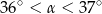 B)
B) 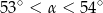 C)
C) 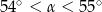 D)
D) 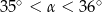
Funkcja 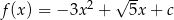 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 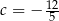 B)
B) 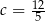 C)
C) 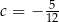 D)
D) 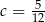
Równanie 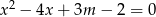 dokładnie jedno rozwiązanie gdy
dokładnie jedno rozwiązanie gdy
A) 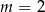 B)
B) 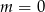 C)
C) 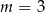 D)
D) 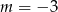
Funkcja kwadratowa 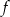 określona wzorem
określona wzorem 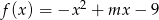 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 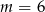 B)
B) 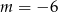 C)
C) 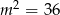 D)
D) 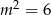
Dla pewnego argumentu funkcje 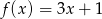 i
i 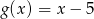 przyjmują taką samą wartość. Jaka to wartość?
przyjmują taką samą wartość. Jaka to wartość?
A) 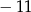 B)
B) 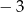 C) 3 D)
C) 3 D) 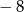
Liczba 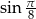 jest równa
jest równa
A) 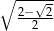 B)
B) 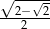 C)
C) 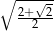 D)
D)