Promień okręgu opisanego na prostokącie o bokach: 6 cm i 8 cm jest równy:
A) 7 cm B) 6,5 cm C) 5 cm D) 10 cm
/Szkoła średnia/Zadania testowe
Wyrażenie 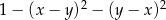 jest równe
jest równe
A) 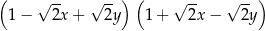 B)
B) 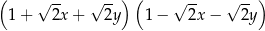
C) 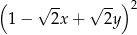 D)
D) 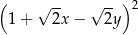
Dany jest sześcian 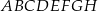 . Przekątne
. Przekątne 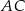 i
i 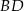 ściany
ściany 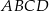 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 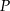 (zobacz rysunek).
(zobacz rysunek).
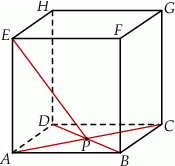
Tangens kąta, jaki odcinek 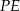 tworzy z płaszczyzną
tworzy z płaszczyzną 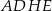 , jest równy
, jest równy
A) 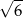 B)
B) 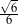 C)
C) 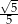 D)
D) 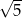
W trójkącie równoramiennym 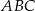 o podstawie
o podstawie 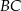 dane są:
dane są: 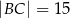 oraz
oraz 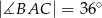 . Odcinek
. Odcinek 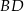 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 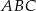 (zobacz rysunek).
(zobacz rysunek).
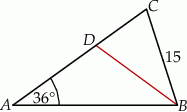
Wówczas długość odcinka 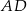 jest równa
jest równa
A) 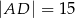 B)
B) 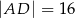 C)
C) 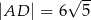 D)
D) 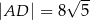
Dla której z liczb wyrażenie 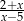 nie ma sensu liczbowego?
nie ma sensu liczbowego?
A) -2 B) -5 C) 0 D) 5
Zbiorem rozwiązań nierówności 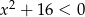 jest zbiór
jest zbiór
A) 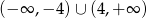 B)
B) 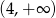 C)
C) 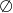 D)
D) 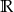
Zbiorem rozwiązań nierówności 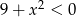 jest zbiór
jest zbiór
A) 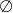 B)
B) 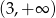 C)
C) 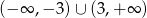 D)
D) 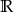
Zbiorem rozwiązań nierówności kwadratowej 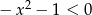 jest
jest
A) 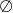 B)
B) 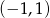 C)
C) 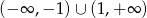 D)
D) 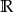
Zbiorem rozwiązań nierówności 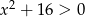 jest zbiór
jest zbiór
A) 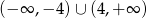 B)
B) 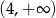 C)
C) 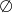 D)
D) 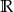
Iloczyn dwóch liczb dodatnich, z których jedna jest o 13 większa od drugiej jest równy 300. Suma tych liczb jest równa
A) 38 B) 13 C) 25 D) 37
Iloczyn dwóch liczb dodatnich, z których jedna jest o 11 większa od drugiej jest równy 350. Suma tych liczb jest równa
A) 39 B) 14 C) 25 D) 37
W pojemniku, w którym znajdowały się same monety 1 złotowe zamieniono 38% monet na monety dwuzłotowe oraz pięciozłotowe, przy czym monet dwuzłotowych było dwa razy więcej niż monet pięciozłotowych. W wyniku tej zamiany kwota pieniędzy zgromadzonych w pudełku zwięszyła się o
A) 58% B) 38% C) 76% D) 48%
Okrąg o równaniu 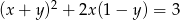 ma promień równy
ma promień równy
A) 3 B) 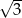 C) 4 D) 2
C) 4 D) 2
Okrąg o równaniu 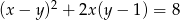 ma promień równy
ma promień równy
A) 9 B) 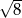 C) 3 D) 8
C) 3 D) 8
Do okręgu należą punkty 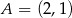 ,
, 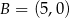 ,
, 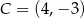 . Jest to okrąg o środku
. Jest to okrąg o środku 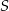 i promieniu
i promieniu  :
:
A) 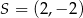 ,
, 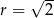 B)
B) 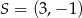 ,
, 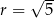
C) 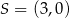 ,
, 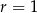 D)
D) 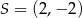 ,
, 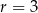
Suma dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego
Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru 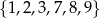 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
Wszystkich liczb naturalnych trzycyfrowych, mniejszych od 600, w których każda cyfra należy do zbioru 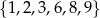 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
Funkcja 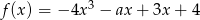 jest funkcją malejąca jeżeli
jest funkcją malejąca jeżeli
A) 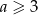 B)
B) 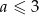 C)
C) 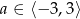 D)
D) 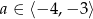
Funkcja 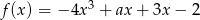 jest funkcją malejąca jeżeli
jest funkcją malejąca jeżeli
A) 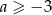 B)
B) 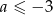 C)
C) 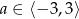 D)
D) 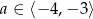
Przekątna 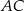 trapezu równoramiennego
trapezu równoramiennego 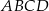 jest prostopadła do ramienia
jest prostopadła do ramienia 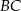 oraz tworzy z ramieniem
oraz tworzy z ramieniem 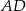 kąt ostry
kąt ostry  . Wysokość trapezu opuszczona z wierzchołka
. Wysokość trapezu opuszczona z wierzchołka 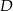 i ramię
i ramię 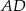 przecinają się pod kątem ostrym
przecinają się pod kątem ostrym 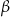 o mierze
o mierze 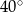 (zobacz rysunek).
(zobacz rysunek).
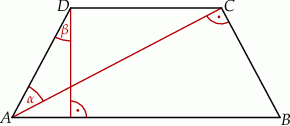
Wtedy kąt  ma miarę
ma miarę
A) 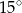 B)
B) 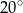 C)
C) 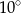 D)
D) 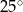
Wykres funkcji 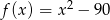 ma dokładnie jeden punkt wspólny z prostą o równaniu
ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 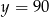 B)
B) 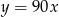 C)
C) 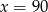 D)
D) 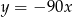
Dana jest funkcja kwadratowa 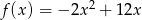 . Wykres tej funkcji ma dokładnie jeden punkt wspólny z prostą o równaniu
. Wykres tej funkcji ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 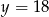 B)
B) 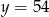 C)
C) 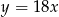 D)
D) 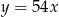
Wykres funkcji 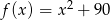 ma dokładnie jeden punkt wspólny z prostą o równaniu
ma dokładnie jeden punkt wspólny z prostą o równaniu
A) 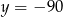 B)
B) 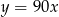 C)
C) 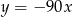 D)
D) 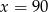
Która z podanych prostych jest styczna do okręgu 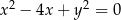 ?
?
A) 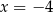 B)
B) 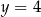 C)
C) 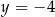 D)
D) 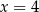
Która z podanych prostych jest styczna do okręgu 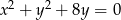 ?
?
A) 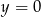 B)
B) 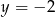 C)
C) 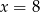 D)
D) 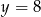
Oś 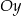 kartezjańskiego układu współrzędnych jest osią symetrii czworokąta
kartezjańskiego układu współrzędnych jest osią symetrii czworokąta 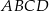 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek jednej z przekątnych czworokąta 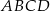 musi leżeć na osi musi leżeć na osi 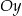 . . | P | F |
Czworokąt 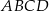 musi być trapezem. musi być trapezem. | P | F |
Średnicą okręgu jest odcinek 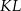 , gdzie
, gdzie 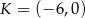 i
i 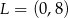 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 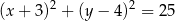 B)
B) 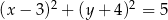
C) 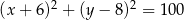 D)
D) 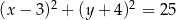
Okrąg o równaniu 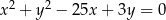 przecina oś
przecina oś 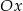 w punktach
w punktach
A) 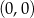 i
i 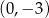 B)
B) 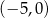 i
i 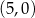
C) 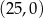 i
i 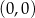 D)
D) 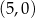 i
i 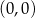
Okrąg o równaniu 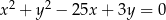 przecina oś
przecina oś 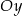 w punktach
w punktach
A) 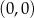 i
i 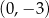 B)
B) 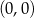 i
i 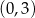
C) 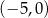 i
i 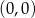 D)
D) 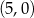 i
i 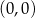
Pierwszy wyraz rosnącego ciągu geometrycznego 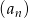 jest równy
jest równy 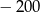 , a iloraz tego ciągu należy do zbioru
, a iloraz tego ciągu należy do zbioru 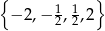 . Wobec tego iloraz ciągu
. Wobec tego iloraz ciągu 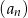 jest równy
jest równy
A) -2 B) 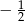 C)
C) 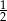 D) 2
D) 2
Pierwszy wyraz malejącego ciągu geometrycznego 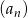 jest równy
jest równy 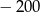 , a iloraz tego ciągu należy do zbioru
, a iloraz tego ciągu należy do zbioru 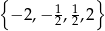 . Wobec tego iloraz ciągu
. Wobec tego iloraz ciągu 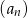 jest równy
jest równy
A) -2 B) 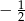 C)
C) 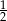 D) 2
D) 2

