Ostrosłup ma tyle samo krawędzi bocznych, ile przekątnych ma jego podstawa. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 5 B) 6 C) 12 D) 10
/Szkoła średnia/Zadania testowe/Geometria
W układzie współrzędnych dany jest okrąg  o równaniu
o równaniu
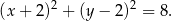
Okrąg  przecina prostą
przecina prostą 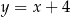 w punktach o współrzędnych
w punktach o współrzędnych
A) 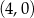 i
i 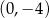 B)
B) 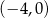 i
i 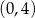
C) 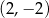 i
i 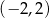 D)
D) 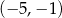 i
i 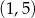
Które z podanych równań jest równaniem prostej.
A) 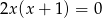 B)
B) 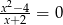 C)
C) 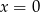 D)
D) 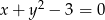
Które z podanych równań nie jest równaniem prostej.
A) 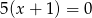 B)
B) 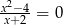 C)
C) 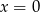 D)
D) 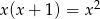
Które z podanych równań jest równaniem prostej.
A) 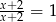 B)
B) 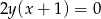 C)
C) 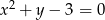 D)
D) 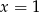
Odcinki 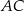 i
i 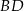 są równoległe, a długości odcinków
są równoległe, a długości odcinków 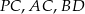 są podane na rysunku.
są podane na rysunku.
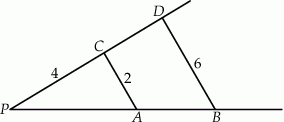
Długość odcinka 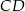 jest równa
jest równa
A) 8 B) 12 C) 6 D) 4
Odcinki 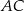 i
i 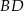 są równoległe, a długości odcinków
są równoległe, a długości odcinków 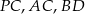 są podane na rysunku.
są podane na rysunku.
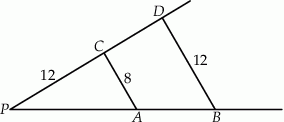
Długość odcinka 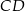 jest równa
jest równa
A) 18 B) 5 C) 7 D) 6
Odcinki 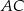 i
i 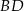 są równoległe, a długości odcinków
są równoległe, a długości odcinków 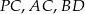 są podane na rysunku.
są podane na rysunku.
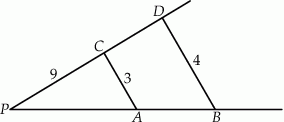
Długość odcinka 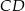 jest równa
jest równa
A) 3 B) 5 C) 2 D) 1
Odległość punktu 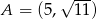 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 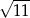 C)
C) 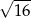 D) 5
D) 5
Odległość punktu 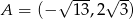 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 1 C) 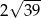 D) 5
D) 5
Odległość punktu 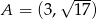 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 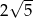 C)
C) 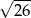 D) 5
D) 5
Wskaż równanie symetralnej odcinka 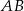 , gdy
, gdy 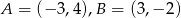 .
.
A) 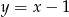 B)
B) 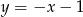 C)
C) 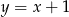 D)
D) 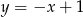
Wskaż równanie symetralnej odcinka 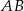 , gdy
, gdy 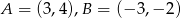 .
.
A) 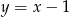 B)
B) 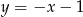 C)
C) 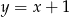 D)
D) 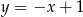
Wskaż równanie symetralnej odcinka 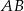 , gdy
, gdy 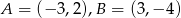 .
.
A) 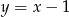 B)
B) 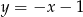 C)
C) 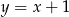 D)
D) 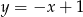
Symetralna odcinka 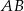 , gdzie
, gdzie 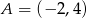 ,
, 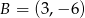 ma równanie
ma równanie
A) 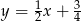 B)
B) 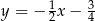 C)
C) 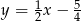 D)
D) 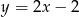
Punkty 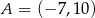 i
i 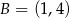 są końcami średnicy
są końcami średnicy 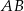 okręgu
okręgu  . Długość okręgu
. Długość okręgu  jest równa
jest równa
A) 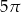 B)
B) 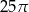 C)
C) 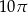 D)
D) 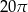
Do okręgu o środku w punkcie 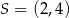 należy punkt
należy punkt 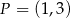 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 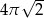 B)
B) 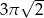 C)
C) 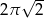 D)
D) 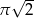
Do okręgu o środku w punkcie 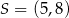 należy punkt
należy punkt 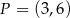 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 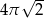 B)
B) 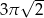 C)
C) 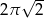 D)
D) 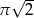
Dany jest kwadrat 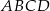 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka 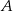 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
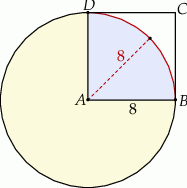
Pole powierzchni części wspólnej koła i kwadratu jest równe
A) 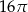 B)
B) 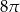 C)
C) 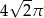 D)
D) 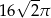
W kwadrat wpisano okrąg o promieniu 6 cm. Obwód tego kwadratu jest równy:
A) 12 cm B) 24 cm C) 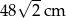 D) 48 cm
D) 48 cm
Kąt wpisany oparty na łuku okręgu długości 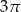 ma miarę
ma miarę 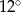 . Jakie jest pole koła ograniczonego tym okręgiem?
. Jakie jest pole koła ograniczonego tym okręgiem?
A) 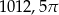 B)
B) 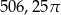 C)
C) 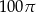 D)
D) 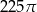
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 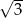 B)
B) 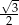 C)
C) 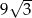 D)
D) 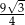
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 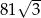 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 27 B) 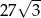 C) 243 D)
C) 243 D) 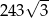
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 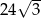 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 8 B) 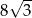 C)
C) 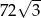 D) 72
D) 72
Okrąg o środku w punkcie 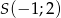 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 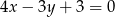 . Promień okręgu jest równy:
. Promień okręgu jest równy:
A)  B) 1 C)
B) 1 C)  D)
D) 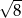
Suma długości wszystkich krawędzi i wszystkich przekątnych ścian sześcianu jest równa 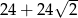 . Jaka jest objętość tego sześcianu?
. Jaka jest objętość tego sześcianu?
A) 8 B) 27 C) 64 D) 96
Suma długości wszystkich krawędzi sześcianu jest o 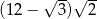 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 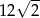 B) 12 C) 2 D)
B) 12 C) 2 D) 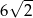
W trójkącie prostokątnym 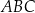 sinus kąta
sinus kąta 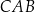 jest równy
jest równy  , a przeciwprostokątna
, a przeciwprostokątna 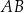 jest o 8 dłuższa od przyprostokątnej
jest o 8 dłuższa od przyprostokątnej 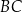 . Długość przeciwprostokątnej
. Długość przeciwprostokątnej 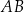 tego trójkąta jest równa
tego trójkąta jest równa
A) 18 B) 20 C) 24 D) 25
Dany jest trójkąt równoramienny 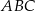 , w którym
, w którym 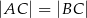 . Na podstawie
. Na podstawie 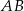 tego trójkąta leży punkt
tego trójkąta leży punkt 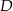 , taki że
, taki że 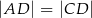 ,
, 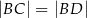 (zobacz rysunek).
(zobacz rysunek).
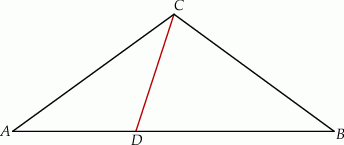
Wynika stąd, że kąt 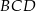 ma miarę
ma miarę
A) 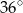 B)
B) 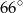 C)
C) 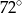 D)
D) 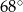
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 58. Ile krawędzi ma ten ostrosłup?
A) 29 B) 14 C) 28 D) 15
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 54. Ile krawędzi ma ten ostrosłup?
A) 26 B) 13 C) 28 D) 14
Punkty 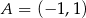 i
i 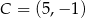 są wierzchołkami rombu
są wierzchołkami rombu 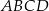 , a prosta określona równaniem
, a prosta określona równaniem 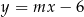 zawiera przekątną
zawiera przekątną 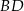 tego rombu. Wynika stąd, że
tego rombu. Wynika stąd, że
A) 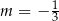 B)
B) 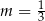 C)
C) 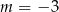 D)
D) 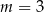
Punkty 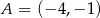 i
i 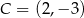 są wierzchołkami rombu
są wierzchołkami rombu 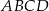 . Wierzchołki
. Wierzchołki 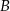 i
i 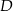 tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 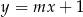 . Zatem
. Zatem
A) 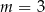 B)
B) 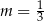 C)
C) 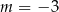 D)
D) 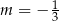
Punkty 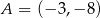 i
i 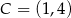 są wierzchołkami rombu
są wierzchołkami rombu 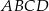 . Wierzchołki
. Wierzchołki 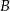 i
i 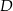 tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 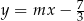 . Zatem
. Zatem
A) 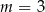 B)
B) 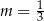 C)
C) 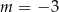 D)
D) 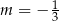
W trójkącie równoramiennym ramię ma długość 5, a kąt ostry przy podstawie jest równy  . Wysokość poprowadzona na podstawę trójkąta wynosi
. Wysokość poprowadzona na podstawę trójkąta wynosi
A) 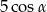 B)
B) 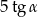 C)
C) 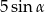 D)
D) 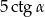
Liczba różnych wartości parametru  , dla których prosta
, dla których prosta 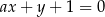 jest prostopadła do prostej
jest prostopadła do prostej 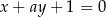 jest
jest
A) równa 0 B) równa 1 C) równa 2 D) większa od 2

