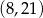Długość odcinka 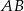 o końcach
o końcach 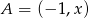 i
i 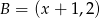 jest równa 6. Wtedy
jest równa 6. Wtedy
A) 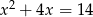 B)
B) 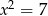 C)
C) 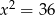 D)
D)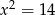
/Szkoła średnia/Zadania testowe/Geometria
Punkt 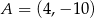 oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
A) 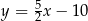 B)
B) 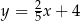 C)
C) 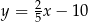 D)
D) 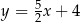
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 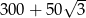 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 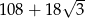 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
W trapezie 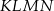 , w którym
, w którym 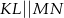 , kąt
, kąt 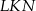 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 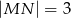 ,
, 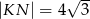 ,
, 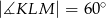 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
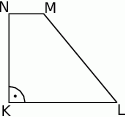
A) 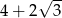 B)
B) 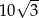 C)
C) 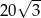 D)
D) 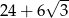
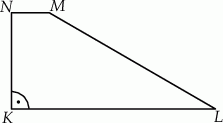
Pole trapezu prostokątnego 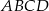 przedstawionego na rysunku, jest równe
przedstawionego na rysunku, jest równe
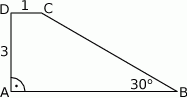
A) 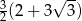 B)
B) 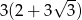 C)
C) 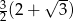 D)
D) 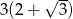
W trapezie 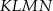 , w którym
, w którym 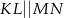 , kąt
, kąt 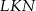 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 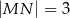 ,
, 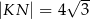 ,
, 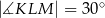 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A)  B)
B) 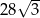 C)
C) 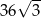 D)
D) 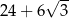
Jeżeli proste 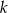 i
i 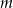 są równoległe (patrz rysunek), to długość odcinka
są równoległe (patrz rysunek), to długość odcinka  wynosi
wynosi
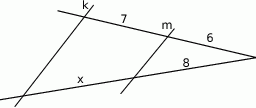
A) 9 B) 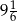 C)
C) 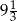 D)
D) 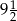
Proste 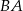 i
i 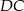 są równoległe. Długości odcinków
są równoległe. Długości odcinków 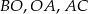 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 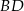 wynosi
wynosi
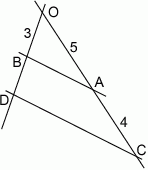
A) 10 B) 2,4 C) 5,4 D) 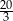
Odcinki 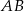 i
i 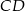 są równoległe (zobacz rysunek). Długość odcinka
są równoległe (zobacz rysunek). Długość odcinka 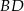 jest równa
jest równa
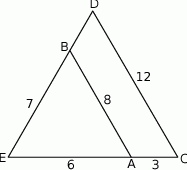
A)  B)
B) 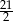 C) 3 D) 2
C) 3 D) 2
Kąt środkowy okręgu jest większy od kąta wpisanego opartego na tym samym łuku, o
A) 200% B) 150% C) 100% D) 50%
Kąt wpisany okręgu jest mniejszy od kąta środkowego opartego na tym samym łuku, o
A) 25% B) 50% C) 100% D) 150%
Dany jest ostrosłup prawidłowy trójkątny 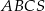 o podstawie
o podstawie 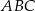 . Punkty
. Punkty 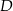 ,
, 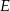 i
i 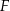 są środkami – odpowiednio – krawędzi bocznych
są środkami – odpowiednio – krawędzi bocznych 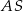 ,
, 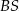 i
i 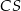 (zobacz rysunek).
(zobacz rysunek).
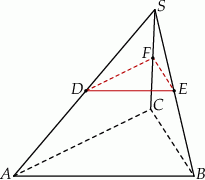
Stosunek objętości ostrosłupa 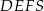 do objętości ostrosłupa
do objętości ostrosłupa 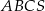 jest równy
jest równy
A) 3 : 4 B) 1 : 4 C) 1 : 8 D) 3 : 8
Dany jest ostrosłup prawidłowy trójkątny 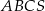 o podstawie
o podstawie 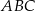 . Punkty
. Punkty 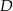 ,
, 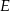 i
i 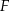 są punktami – odpowiednio – krawędzi bocznych
są punktami – odpowiednio – krawędzi bocznych 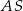 ,
, 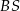 i
i 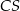 takimi, że
takimi, że 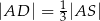 ,
, 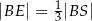 i
i 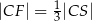 (zobacz rysunek).
(zobacz rysunek).
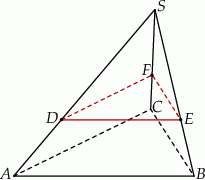
Stosunek objętości ostrosłupa 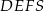 do objętości ostrosłupa
do objętości ostrosłupa 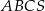 jest równy
jest równy
A) 8 : 27 B) 2 : 3 C) 8 : 9 D) 4 : 9
Przeciwprostokątna 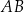 trójkąta prostokątnego
trójkąta prostokątnego 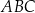 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
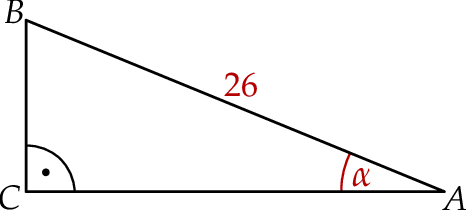
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 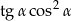 jest równa
jest równa
A) 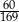 B)
B) 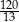 C)
C) 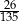 D)
D) 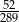
Długości boków prostokąta są równe 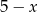 i
i 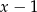 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 1 C) 4 D) 3
Długości boków prostokąta są równe 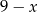 i
i 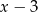 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 7 B) 6 C) 4 D) 5
Długości boków prostokąta są równe 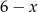 i
i 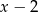 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 5 C) 4 D) 3
Znajdź skalę podobieństwa trójkąta 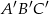 do trójkąta
do trójkąta 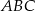 :
:
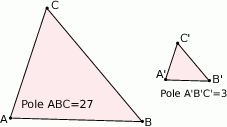
A) 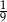 B)
B) 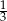 C) 3 D) 9
C) 3 D) 9
Znajdź skalę podobieństwa trójkąta 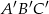 do trójkąta
do trójkąta 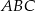 :
:
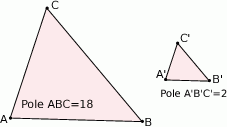
A) 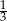 B)
B) 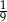 C) 3 D) 9
C) 3 D) 9
Dłuższy bok prostokąta ma długość 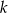 . Przekątna prostokąta tworzy z krótszym bokiem kąt
. Przekątna prostokąta tworzy z krótszym bokiem kąt  . Długość przekątnej prostokąta wynosi
. Długość przekątnej prostokąta wynosi
A) 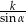 B)
B) 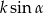 C)
C) 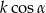 D)
D) 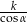
W trapezie równoramiennym kąt ostry ma miarę 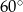 , a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
, a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
A) 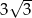 B)
B) 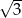 C)
C)  D)
D) 
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
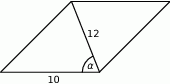
Wtedy
A) 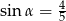 B)
B) 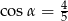 C)
C) 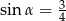 D)
D) 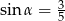
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
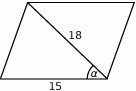
Wtedy
A) 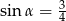 B)
B) 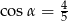 C)
C) 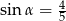 D)
D) 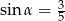
Z prostopadłościanu 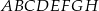 odcięto ostrosłup
odcięto ostrosłup 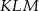 w ten sposób, że punkty
w ten sposób, że punkty 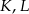 i
i 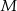 są środkami krawędzi
są środkami krawędzi 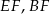 i
i 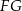 (zobacz rysunek).
(zobacz rysunek).
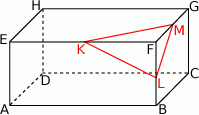
Ile razy objętość odciętego ostrosłupa jest mniejsza od objętości pozostałej części prostopadłościanu?
A) 48 razy. B) 47 razy. C) 46 razy. D) 24 razy.
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 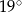 i
i 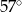 .
.
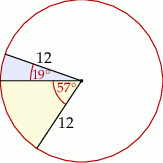
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 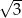
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
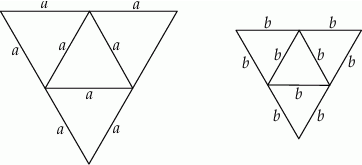
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 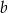 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 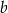 ?
?
A) 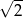 B) 2 C)
B) 2 C) 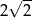 D) 4
D) 4
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
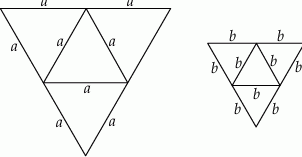
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 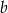 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 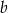 ?
?
A) 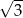 B)
B) 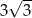 C) 3 D) 9
C) 3 D) 9
Odległość początku układu współrzędnych od prostej o równaniu 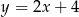 jest równa
jest równa
A) 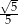 B)
B) 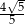 C)
C)  D) 4
D) 4
Odległość początku układu współrzędnych od prostej o równaniu 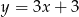 jest równa
jest równa
A) 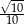 B)
B) 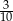 C)
C) 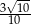 D) 3
D) 3
Odległość początku układu współrzędnych od prostej o równaniu 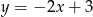 jest równa
jest równa
A) 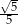 B) 3 C)
B) 3 C)  D)
D) 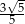
Odległość początku układu współrzędnych od prostej o równaniu 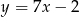 jest równa
jest równa
A) 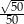 B)
B) 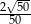 C)
C) 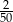 D) 2
D) 2
Odległość początku układu współrzędnych od prostej o równaniu 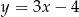 jest równa
jest równa
A) 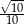 B) 4 C)
B) 4 C) 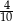 D)
D) 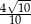
Odległość początku układu współrzędnych od prostej o równaniu 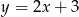 jest równa
jest równa
A) 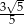 B)
B) 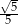 C)
C)  D) 3
D) 3
Punkt 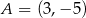 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 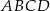 , a punkt
, a punkt 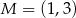 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 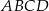 jest równe
jest równe
A) 68 B) 136 C) 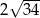 D)
D) 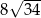
Punkt 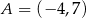 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 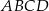 , a punkt
, a punkt 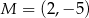 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 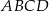 jest równe
jest równe
A) 360 B) 90 C) 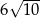 D)
D) 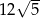
Odcinek 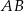 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 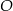 i promieniu
i promieniu 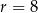 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 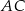 ma długość
ma długość 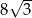 .
.
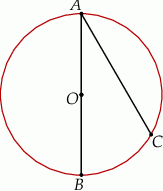
Miara kąta 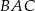 jest równa
jest równa
A) 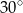 B)
B) 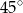 C)
C) 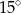 D)
D) 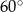
Odcinek 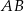 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 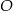 i promieniu
i promieniu 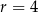 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 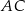 ma długość
ma długość 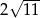 .
.
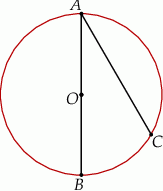
Sinus kąta 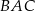 jest równy
jest równy
A) 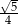 B)
B) 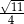 C)
C) 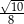 D)
D) 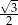
Punkty 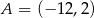 ,
, 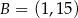 i
i 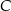 leżą na jednej prostej. Punkt
leżą na jednej prostej. Punkt 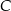 może mieć współrzędne
może mieć współrzędne
A) 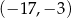 B)
B) 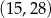 C)
C) 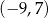 D)
D)