W trójkącie 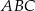 bok
bok 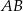 ma długość 4, a bok
ma długość 4, a bok 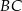 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 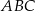 przecina bok
przecina bok 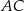 w punkcie
w punkcie 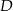 takim, że
takim, że 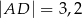 (zobacz rysunek).
(zobacz rysunek).
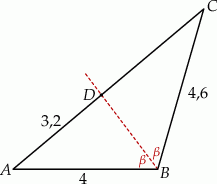
Odcinek 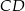 ma długość
ma długość
A) 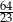 B)
B) 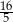 C)
C) 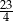 D)
D) 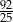
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 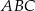 bok
bok 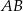 ma długość 4, a bok
ma długość 4, a bok 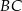 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 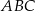 przecina bok
przecina bok 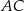 w punkcie
w punkcie 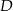 takim, że
takim, że 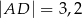 (zobacz rysunek).
(zobacz rysunek).

Odcinek 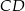 ma długość
ma długość
A) 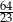 B)
B) 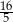 C)
C) 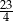 D)
D) 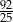
Krawędź sześcianu ma długość 9. Długość przekątnej tego sześcianu jest równa:
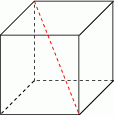
A) 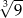 B)
B) 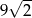 C)
C) 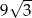 D)
D) 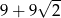
Krawędź sześcianu ma długość 6. Długość przekątnej tego sześcianu jest równa:
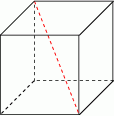
A) 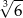 B)
B) 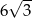 C)
C) 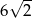 D)
D) 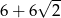
Punkt 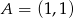 jest wierzchołkiem rombu
jest wierzchołkiem rombu 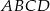 . Prosta o równaniu
. Prosta o równaniu 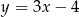 zawiera przekątną
zawiera przekątną 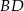 . Przekątna
. Przekątna 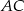 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 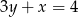 B)
B) 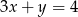 C)
C) 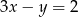 D)
D) 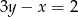
Punkt 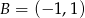 jest wierzchołkiem rombu
jest wierzchołkiem rombu 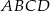 . Prosta o równaniu
. Prosta o równaniu 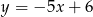 zwiera przekątną
zwiera przekątną 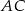 . Przekątna
. Przekątna 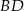 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 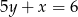 B)
B) 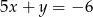 C)
C) 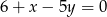 D)
D) 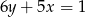
W trójkąt równoboczny wpisano okrąg o równaniu 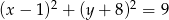 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 9 B) 27 C) 4,5 D) 1
W trójkąt równoboczny wpisano okrąg o równaniu 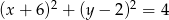 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 12 B) 6 C) 8 D) 4
W trójkąt równoboczny wpisano okrąg o równaniu 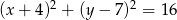 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 48 B) 32 C) 24 D) 12
W kartezjańskim układzie współrzędnych 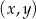 dany jest kwadrat
dany jest kwadrat 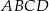 . Wierzchołki
. Wierzchołki 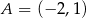 i
i 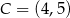 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 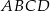 jest równa
jest równa
A) 10 B) 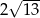 C)
C) 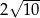 D) 8
D) 8
W kartezjańskim układzie współrzędnych 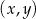 dany jest kwadrat
dany jest kwadrat 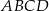 . Wierzchołki
. Wierzchołki 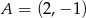 i
i 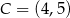 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 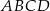 jest równa
jest równa
A) 10 B) 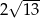 C)
C) 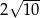 D) 8
D) 8
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 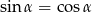 . Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
A) 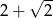 B)
B) 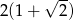 C)
C) 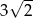 D)
D) 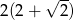
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 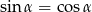 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 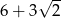 B)
B) 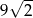 C)
C) 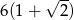 D)
D) 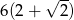
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 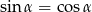 . Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
A) 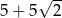 B)
B) 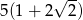 C)
C) 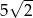 D)
D) 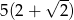
Odcinki 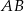 i
i 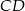 są równoległe. Długości odcinków
są równoległe. Długości odcinków 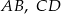 i
i 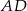 są podane na rysunku.
są podane na rysunku.
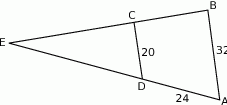
Długość odcinka 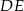 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
Odcinki 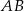 i
i 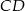 są równoległe i
są równoległe i 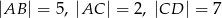 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 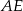 jest równa
jest równa
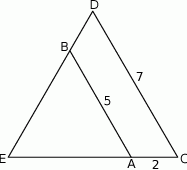
A) 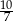 B)
B) 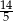 C) 3 D) 5
C) 3 D) 5
Odcinki 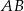 i
i 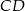 są równoległe. Długości odcinków
są równoległe. Długości odcinków 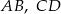 i
i 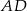 są podane na rysunku.
są podane na rysunku.
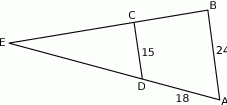
Długość odcinka 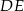 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
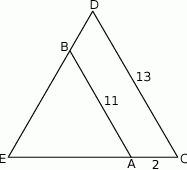
Odcinki 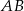 i
i 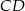 są równoległe i
są równoległe i 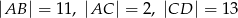 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 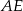 jest równa
jest równa
A) 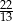 B)
B) 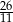 C) 11 D) 13
C) 11 D) 13
Kąt między ramionami trójkąta równoramiennego ma miarę 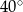 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 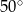 B)
B) 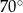 C)
C) 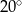 D)
D) 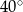
Kąt między ramionami trójkąta równoramiennego ma miarę 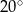 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 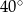 B)
B) 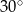 C)
C) 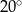 D)
D) 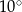
Dany jest trójkąt 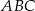 , w którym
, w którym 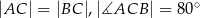 , zaś
, zaś 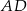 jest wysokością trójkąta. Wówczas miara kąta
jest wysokością trójkąta. Wówczas miara kąta 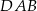 wynosi
wynosi
A) 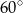 B)
B) 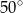 C)
C) 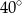 D)
D) 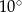
Kąt między ramionami trójkąta równoramiennego ma miarę 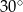 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 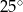 B)
B) 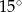 C)
C) 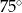 D)
D) 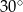
Kąt między ramionami trójkąta równoramiennego wynosi 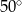 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 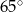 B)
B) 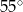 C)
C) 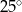 D)
D) 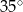
Kąt między ramionami trójkąta równoramiennego wynosi 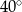 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 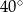 B)
B) 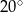 C)
C) 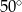 D)
D) 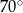
Proste o równaniach 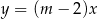 oraz
oraz 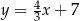 przecinają się w jednym punkcie Wtedy
przecinają się w jednym punkcie Wtedy
A) 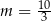 B)
B) 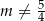 C)
C) 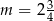 D)
D) 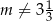
Przekątna ściany sześcianu ma długość 8. Przekątna tego sześcianu ma długość
A) 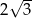 B)
B) 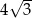 C)
C) 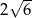 D)
D) 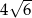
Przekątna ściany sześcianu ma długość 6. Przekątna tego sześcianu ma długość
A) 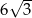 B)
B) 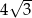 C)
C) 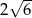 D)
D) 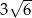
Przekątna ściany sześcianu ma długość 10. Przekątna tego sześcianu ma długość
A) 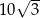 B)
B) 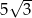 C)
C) 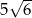 D)
D) 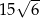
Przekątna ściany sześcianu ma długość 12. Przekątna tego sześcianu ma długość
A) 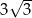 B)
B) 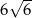 C)
C) 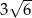 D)
D) 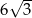
W trójkącie równobocznym 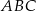 poprowadzono odcinki
poprowadzono odcinki 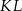 i
i 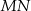 , które podzieliły boki
, które podzieliły boki 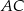 i
i 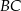 na trzy równe części. Stosunek pola trójkąta
na trzy równe części. Stosunek pola trójkąta 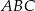 do pola trapezu
do pola trapezu 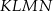 jest równy
jest równy
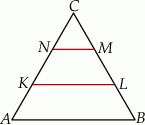
A) 3 B) 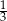 C) 9 D) 6
C) 9 D) 6
Wskaż wektor równoległy do wektora ![→ v = [− 72 ,9 6]](https://img.zadania.info/zad/4179753/HzadT0x.gif)
A) ![[48,36]](https://img.zadania.info/zad/4179753/HzadT1x.gif) B)
B) ![[45,− 60 ]](https://img.zadania.info/zad/4179753/HzadT2x.gif) C)
C) ![[− 42,64]](https://img.zadania.info/zad/4179753/HzadT3x.gif) D)
D) ![[76,− 57 ]](https://img.zadania.info/zad/4179753/HzadT4x.gif)
Kąt wpisany w okrąg o promieniu 10 ma miarę 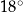 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 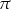 B)
B) 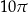 C)
C) 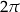 D)
D) 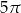
Kąt wpisany w okrąg o promieniu 9 ma miarę 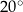 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 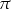 B)
B) 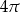 C)
C) 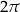 D)
D) 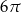
Kąt wpisany w okrąg o promieniu 8 ma miarę 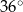 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 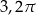 B)
B) 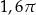 C)
C) 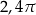 D)
D) 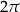
Kąt wpisany w okrąg o promieniu 9 ma miarę 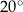 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 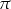 B)
B) 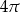 C)
C) 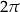 D)
D) 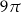
Długość odcinka  jest równa
jest równa
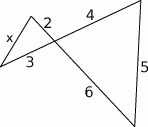
A) 1 B) 2,5 C) 2 D) 1,5
Długość odcinka 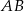 , równoległego do odcinka
, równoległego do odcinka 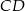 , jest równa:
, jest równa:
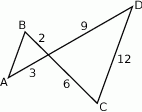
A) 6 B) 3 C) 2 D) 4
Długość odcinka  jest równa
jest równa
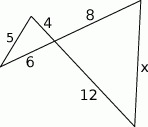
A) 12 B) 15 C) 10 D) 8
Długość odcinka  jest równa
jest równa
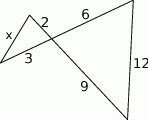
A) 4 B) 2 C) 3 D) 6
Długość odcinka  jest równa
jest równa
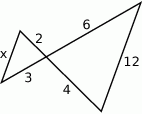
A) 6 B) 3 C) 2 D) 4
Długość odcinka  jest równa
jest równa
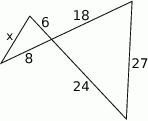
A) 9 B) 8 C) 12 D) 7,5
Okrąg opisany na trójkącie równobocznym ma promień równy 6. Wysokość tego trójkąta jest równa
A) 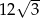 B) 18 C) 9 D)
B) 18 C) 9 D) 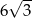
Okrąg opisany na trójkącie równobocznym ma promień równy 8. Wysokość tego trójkąta jest równa
A) 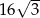 B) 12 C) 24 D)
B) 12 C) 24 D) 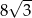
Promień okręgu opisanego na trójkącie równobocznym jest równy 8. Wysokość tego trójkąta jest równa
A) 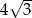 B)
B) 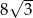 C) 12 D) 6
C) 12 D) 6
Okrąg opisany na trójkącie równobocznym ma promień równy 12. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 22 D) 24
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu 12 cm. Podstawa tego stożka jest kołem o promieniu
A) 12 cm B) 6 cm C) 3 cm D) 1 cm
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano połowę koła o promieniu 6. Promień podstawy tego stożka ma długość
A) 6 B)  C) 3 D)
C) 3 D) 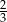
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano jedną czwarta koła o promieniu 6. Promień podstawy tego stożka ma długość
A)  B)
B)  C) 3 D)
C) 3 D) 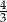
Pole trójkąta równobocznego 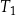 jest równe
jest równe 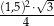 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 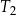 jest równe
jest równe 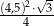 . Trójkąt
. Trójkąt 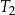 jest podobny do trójkąta
jest podobny do trójkąta 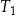 w skali
w skali
| A) 3, | B) 9, |
ponieważ
| 1) | każdy z tych trójkątów ma dokładnie trzy osie symetrii. |
| 2) | pole trójkąta 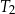 jest 9 razy większe od pola trójkąta jest 9 razy większe od pola trójkąta 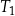 . . |
| 3) | bok trójkąta 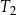 jest o 3 dłuższy od boku trójkąta jest o 3 dłuższy od boku trójkąta 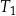 . . |
Pole trójkąta równobocznego 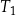 jest równe
jest równe 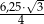 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 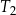 jest równe
jest równe 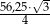 . Trójkąt
. Trójkąt 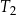 jest podobny do trójkąta
jest podobny do trójkąta 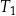 w skali
w skali
| A) 5, | B) 3, |
ponieważ
| 1) | pole trójkąta 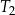 jest 25 razy większe od pola trójkąta jest 25 razy większe od pola trójkąta 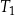 . . |
| 2) | bok trójkąta 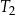 jest o 5 dłuższy od boku trójkąta jest o 5 dłuższy od boku trójkąta 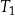 . . |
| 3) | bok trójkąta 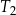 jest 3 razy dłuższy od boku trójkąta jest 3 razy dłuższy od boku trójkąta 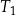 . . |
Wysokość trójkąta równobocznego 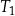 jest równa
jest równa 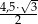 . Wysokość trójkąta równobocznego
. Wysokość trójkąta równobocznego 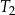 jest równa
jest równa 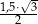 . Stosunek pola trójkąta
. Stosunek pola trójkąta 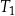 do pola trójkąta
do pola trójkąta 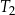 jest równy
jest równy
| A) 3, | B) 9, |
ponieważ
| 1) | bok trójkąta 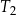 jest 9 razy krótszy od boku trójkąta jest 9 razy krótszy od boku trójkąta 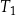 . . |
| 2) | wysokość trójkąta 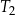 jest 3 razy krótsza od wysokości trójkąta jest 3 razy krótsza od wysokości trójkąta 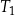 . . |
| 3) | bok trójkąta 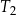 jest o 3 krótszy od boku trójkąta jest o 3 krótszy od boku trójkąta 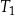 . . |
Wymiary prostopadłościanu 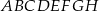 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 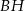 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 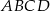 pod kątem
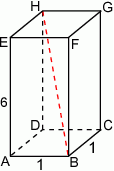
pod kątem  takim, że
takim, że
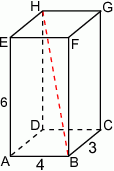
A) 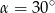 B)
B) 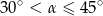 C)
C) 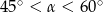 D)
D) 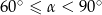
Wymiary prostopadłościanu 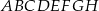 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 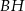 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 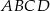 pod kątem
pod kątem  takim, że
takim, że
A) 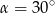 B)
B) 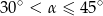 C)
C) 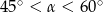 D)
D) 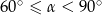
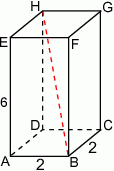
Wymiary prostopadłościanu 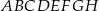 podane są na rysunku. Przekątna
podane są na rysunku. Przekątna 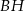 prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy 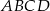 pod kątem
pod kątem  takim, że
takim, że
A) 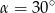 B)
B) 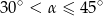 C)
C) 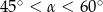 D)
D) 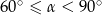
Objętość sześcianu jest równa 64. Przekątna ściany bocznej tego sześcianu ma długość
A) 4 B) 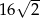 C)
C) 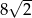 D)
D) 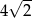
Objętość sześcianu jest równa 27. Przekątna ściany bocznej tego sześcianu ma długość
A) 3 B) 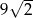 C)
C) 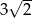 D)
D) 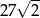
Objętość sześcianu jest równa 125. Przekątna ściany bocznej tego sześcianu ma długość
A) 5 B) 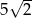 C)
C) 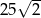 D)
D) 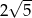
Każdy kąt wewnętrzny sześciokąta 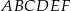 ma miarę
ma miarę 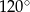 . Bok
. Bok 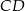 tego sześciokąta jest zwarty w prostej o równaniu
tego sześciokąta jest zwarty w prostej o równaniu 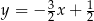 , a punkt
, a punkt 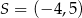 jest środkiem boku
jest środkiem boku 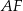 . Bok
. Bok 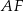 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu
A) 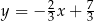 B)
B) 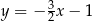 C)
C) 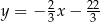 D)
D)