Dany jest trójkąt 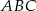 o kącie
o kącie 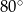 przy wierzchołku
przy wierzchołku 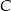 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 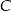 ma miarę
ma miarę 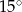 . Wynika stąd, że kąt
. Wynika stąd, że kąt 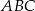 jest równy
jest równy
A) 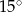 B)
B) 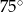 C)
C) 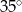 D)
D) 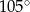
/Szkoła średnia/Zadania testowe/Geometria
Dany jest trójkąt 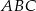 o kącie
o kącie 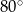 przy wierzchołku
przy wierzchołku 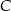 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 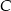 ma miarę
ma miarę 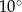 . Wynika stąd, że kąt
. Wynika stąd, że kąt 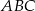 jest równy
jest równy
A) 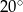 B)
B) 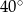 C)
C) 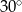 D)
D) 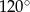
Okrąg o równaniu 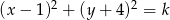 jest styczny do osi
jest styczny do osi 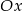 . Liczba
. Liczba 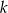 jest równa
jest równa
A) 2 B) 4 C) 8 D) 16
Okrąg opisany równaniem 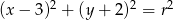 jest styczny do osi
jest styczny do osi 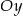 . Promień
. Promień  tego okręgu jest równy
tego okręgu jest równy
A) 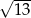 B)
B) 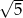 C) 3 D) 2
C) 3 D) 2
Wektor 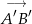 jest obrazem wektora
jest obrazem wektora 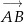 w jednokładności o środku
w jednokładności o środku 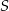 i skali
i skali 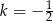 . Zatem
. Zatem
A) 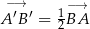 B)
B) 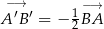 C)
C) 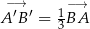 D)
D) 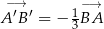
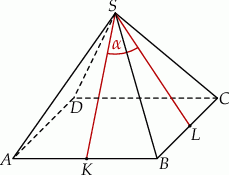
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy długości 80 cm i krawędzi bocznej długości 90 cm (zobacz rysunek), a ponadto dane są cztery odcinki 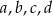 , o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
, o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
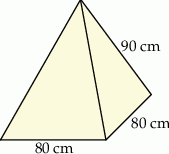
Wysokość tego ostrosłupa jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 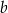 .
.
C) tylko od odcinków 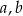 i
i  .
.
D) od wszystkich czterech danych odcinków.
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 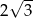 C)
C) 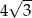 D) 12
D) 12
Promień okręgu wpisanego w trójkąt równoboczny jest o 3 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 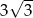 C)
C) 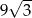 D) 9
D) 9
Dany jest graniastosłup prawidłowy sześciokątny 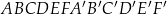 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 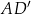 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 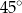 (zobacz rysunek).
(zobacz rysunek).
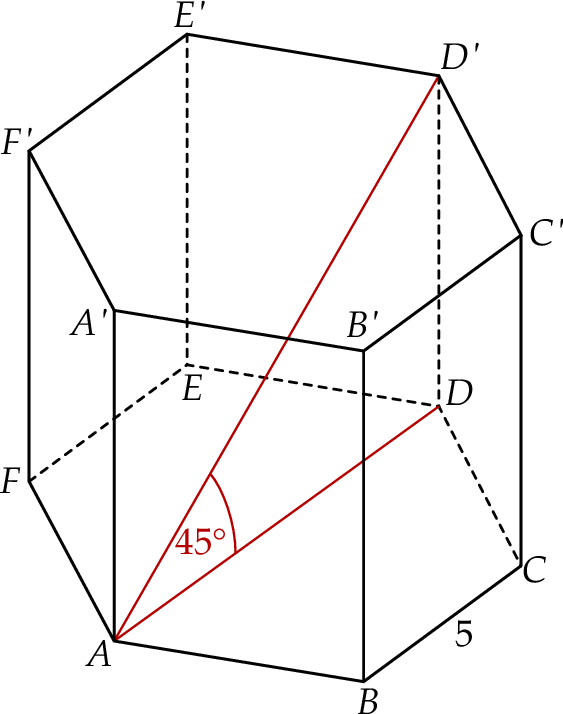
Pole ściany bocznej tego graniastosłupa jest równe
A) 12,5 B) 25 C) 50 D) 100
Dany jest graniastosłup prawidłowy sześciokątny 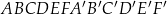 , w którym krawędź podstawy ma długość 3. Przekątna
, w którym krawędź podstawy ma długość 3. Przekątna 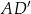 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 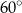 (zobacz rysunek).
(zobacz rysunek).
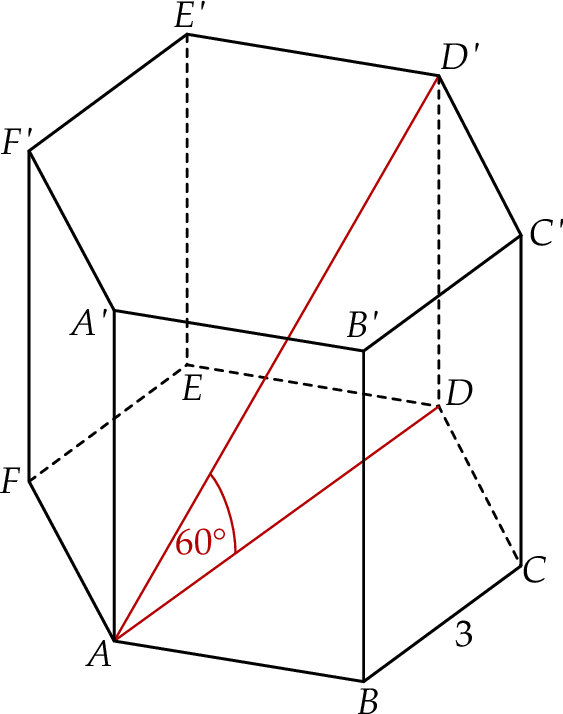
Pole ściany bocznej tego graniastosłupa jest równe
A) 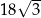 B)
B) 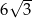 C)
C) 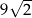 D) 90
D) 90
Przekątna 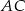 prostokąta
prostokąta 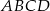 ma długość 11, a bok
ma długość 11, a bok 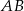 jest od niej o 5 krótszy. Oblicz długość boku
jest od niej o 5 krótszy. Oblicz długość boku 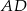 .
.
A) 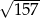 B)
B) 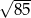 C) 5 D)
C) 5 D) 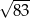
Przekątna 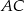 prostokąta
prostokąta 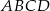 ma długość 14. Bok
ma długość 14. Bok 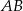 tego prostokąta ma długość 6. Długość boku
tego prostokąta ma długość 6. Długość boku 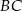 jest równa
jest równa
A) 8 B) 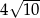 C)
C) 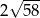 D) 10
D) 10
Przekątna 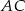 prostokąta
prostokąta 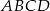 ma długość 13, a bok
ma długość 13, a bok 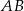 jest od niej o 5 krótszy. Oblicz długość boku
jest od niej o 5 krótszy. Oblicz długość boku 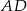 .
.
A) 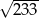 B) 11 C)
B) 11 C) 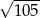 D)
D) 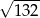
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 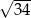 , a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
, a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
A) 4 B) 18 C) 36 D) 24
Ceramiczna ozdoba ma kształt czworościanu foremnego o krawędzi długości 6 dm (zobacz rysunek).
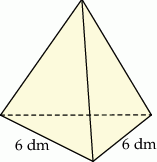
Wysokość tego czworościanu jest – z dokładnością do 0,01 dm – równa
A) 3,46 dm B) 4,9 dm C) 5,2 dm D) 4,8 dm
W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy 7 : 3. Podstawą tego graniastosłupa jest
A) trójkąt. B) pięciokąt. C) siedmiokąt. D) ośmiokąt.
Dany jest trójkąt 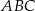 o bokach
o bokach 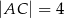 ,
, 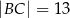 ,
, 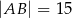 . Sinus kąta
. Sinus kąta 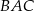 jest równy
jest równy  , a dwusieczne kątów
, a dwusieczne kątów 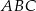 i
i 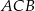 przecinają się w punkcie
przecinają się w punkcie 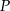 (zobacz rysunek).
(zobacz rysunek).
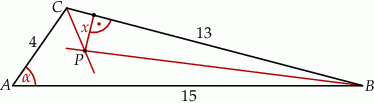
Odległość  punktu
punktu 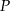 od prostej
od prostej 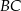 jest równa
jest równa
A) 2 B) 1 C)  D)
D) 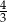
Na rysunku przedstawiono fragment prostej o równaniu 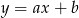 .
.
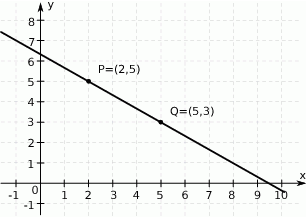
Współczynnik kierunkowy tej prostej jest równy
A) 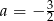 B)
B) 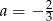 C)
C) 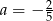 D)
D) 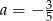
Na rysunku przedstawiono fragment prostej o równaniu 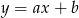 .
.
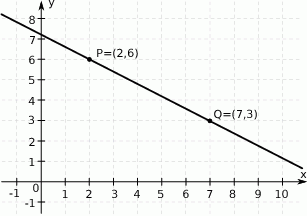
Współczynnik kierunkowy tej prostej jest równy
A) 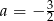 B)
B) 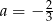 C)
C) 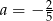 D)
D) 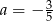
Na rysunku przedstawiono trapez 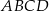 o podstawach
o podstawach 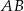 i
i 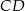 , w którym
, w którym 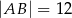 i
i 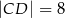 .
.
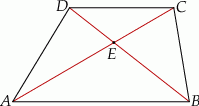
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Pola trójkątów utworzonych przez przekątne trapezu i jego boki spełniają równość
A) 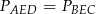 B)
B) 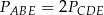 C)
C) 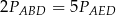
D) 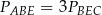 E)
E) 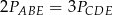 F)
F) 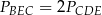
Dany jest okrąg o równaniu 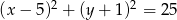 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 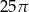 B)
B) 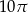 C)
C) 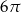 D)
D) 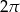
Dany jest okrąg o równaniu 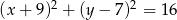 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 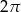 B)
B) 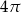 C)
C) 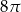 D)
D) 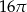
Dany jest okrąg o równaniu 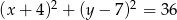 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 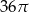 B)
B) 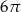 C)
C) 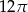 D)
D) 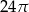
W ostrosłupie prawidłowym czworokątnym 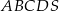 wszystkie krawędzie mają jednakową długość.
wszystkie krawędzie mają jednakową długość.
Oblicz cosinus kąta utworzonego przez wysokości 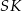 i
i 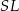 dwóch sąsiednich ścian bocznych.
dwóch sąsiednich ścian bocznych.
Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa 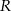 .
.
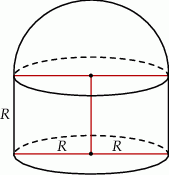
Objętość tej bryły jest równa
A) 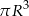 B)
B) 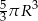 C)
C) 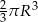 D)
D) 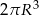
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
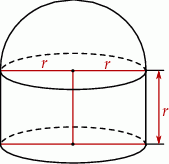
Pole powierzchni całkowitej tej bryły jest równe
A) 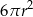 B)
B) 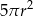 C)
C) 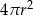 D)
D) 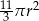
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
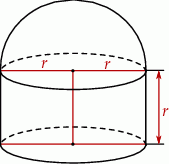
Objętość tej bryły jest równa
A) 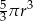 B)
B) 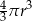 C)
C) 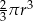 D)
D) 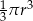
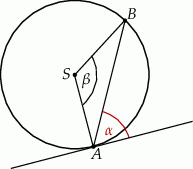
Kąt między cięciwą 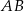 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 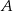 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 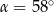 . Wówczas
. Wówczas
A) 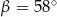 B)
B) 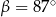 C)
C) 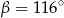 D)
D) 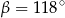
Punkty 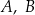 oraz
oraz 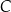 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 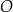 . Prosta
. Prosta 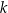 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 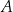 i tworzy z cięciwą
i tworzy z cięciwą 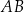 kąt o mierze
kąt o mierze 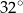 . Ponadto odcinek
. Ponadto odcinek 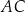 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 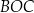 jest równa
jest równa
A) 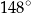 B)
B) 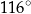 C)
C) 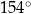 D)
D) 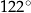
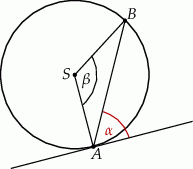
Kąt między cięciwą 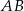 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 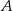 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 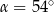 . Wówczas
. Wówczas
A) 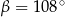 B)
B) 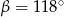 C)
C) 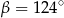 D)
D) 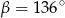
Punkty 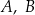 oraz
oraz 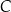 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 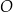 . Prosta
. Prosta 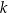 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 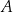 i tworzy z cięciwą
i tworzy z cięciwą 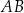 kąt o mierze
kąt o mierze 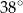 . Ponadto odcinek
. Ponadto odcinek 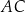 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 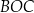 jest równa
jest równa
A) 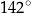 B)
B) 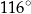 C)
C) 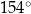 D)
D) 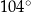
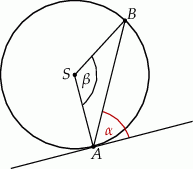
Kąt między cięciwą 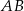 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 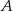 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 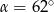 . Wówczas
. Wówczas
A) 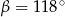 B)
B) 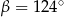 C)
C) 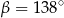 D)
D) 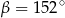
Podstawy trapezu równoramiennego 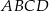 mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).
mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).

Wtedy miara  kąta ostrego
kąta ostrego 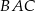 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 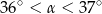 B)
B) 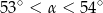 C)
C) 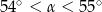 D)
D) 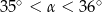
W trójkącie 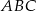 długość środkowej
długość środkowej 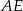 jest równa połowie długości boku
jest równa połowie długości boku 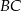 . Wówczas trójkąt
. Wówczas trójkąt 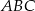 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
W trójkącie 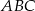 poprowadzono środkową
poprowadzono środkową 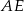 i okazało się, że
i okazało się, że 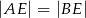 . Zatem trójkąt
. Zatem trójkąt 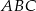 jest trójkątem
jest trójkątem
A) ostrokątnym B) równobocznym C) równoramiennym D) prostokątnym
Dany jest trójkąt prostokątny o kątach ostrych  i
i 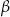 (zobacz rysunek).
(zobacz rysunek).
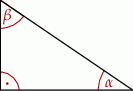
Wyrażenie 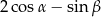 jest równe
jest równe
A) 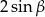 B)
B) 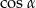 C) 0 D) 2
C) 0 D) 2
Dany jest trójkąt prostokątny o kątach ostrych  i
i 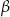 (zobacz rysunek).
(zobacz rysunek).
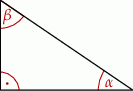
Wyrażenie 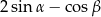 jest równe
jest równe
A) 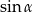 B)
B) 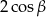 C) 0 D) 2
C) 0 D) 2

