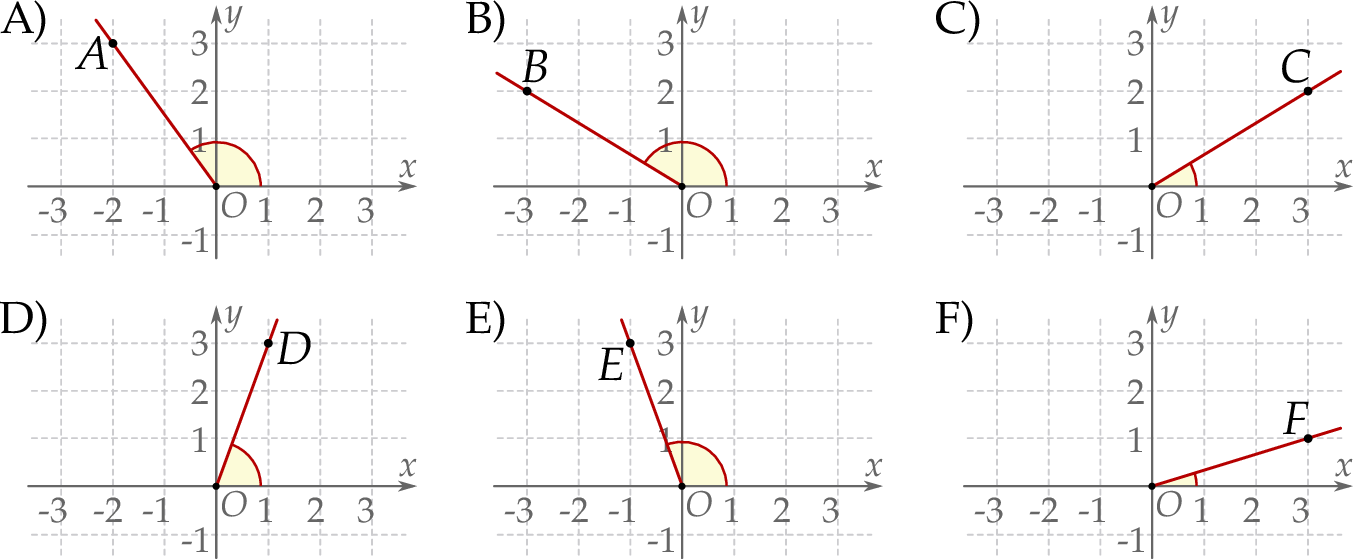
Na rysunkach A–F w kartezjańskim układzie współrzędnych 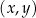 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 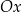 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 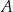 lub
lub 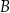 , lub
, lub 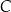 , lub
, lub 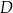 , lub
, lub 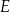 , lub
, lub 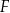 .
.
Kąt 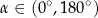 , spełniający warunek
, spełniający warunek 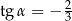 , jest zaznaczony na rysunku …
, jest zaznaczony na rysunku …

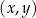 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 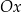 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 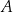 lub
lub 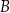 , lub
, lub 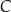 , lub
, lub 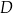 , lub
, lub 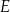 , lub
, lub 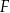 .
. 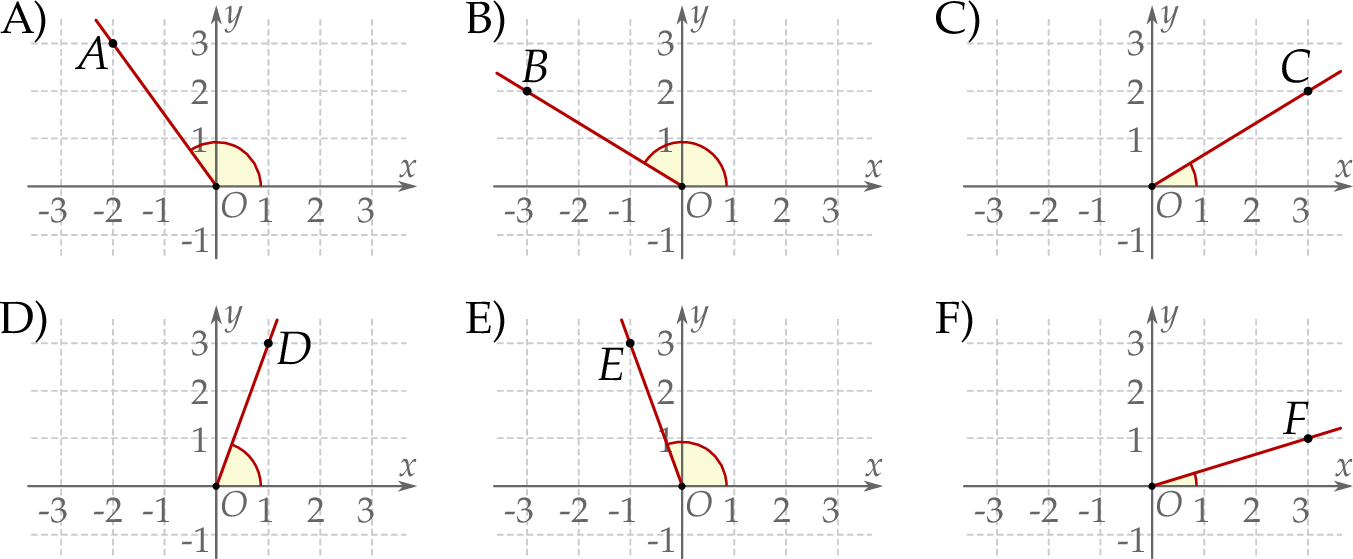
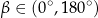 , spełniający warunek
, spełniający warunek 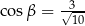 ?
? 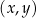 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 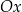 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 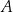 lub
lub 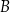 , lub
, lub 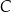 , lub
, lub  , lub
, lub  , lub
, lub  .
. 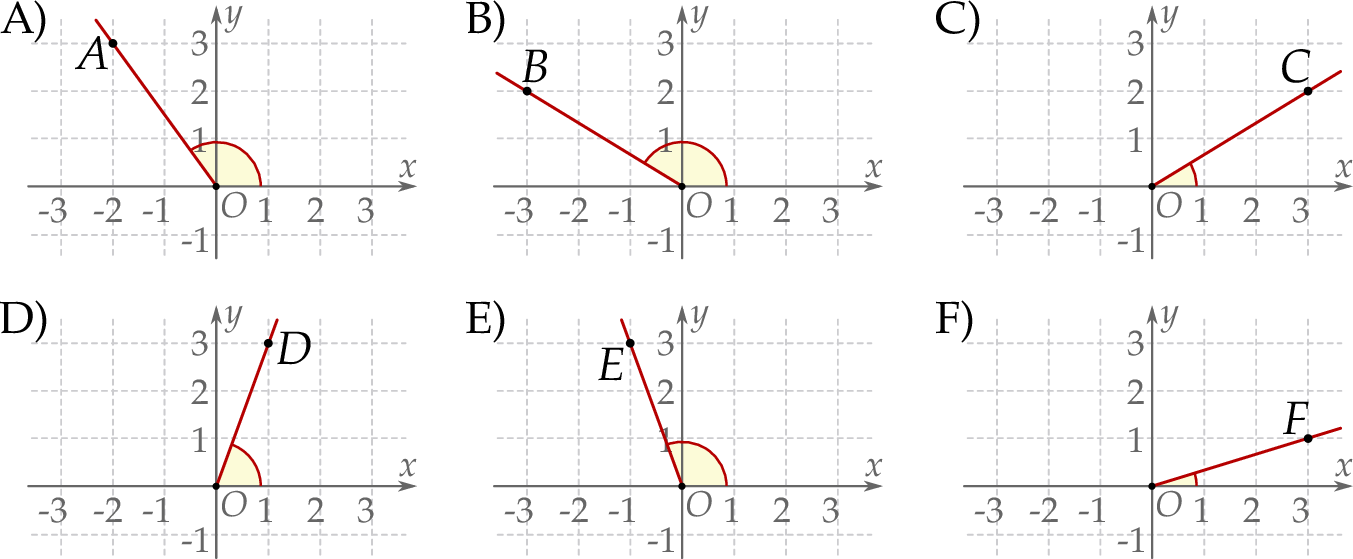
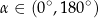 , spełniający warunek
, spełniający warunek 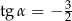 ?
?  zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią  , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 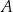 lub
lub 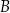 , lub
, lub 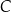 , lub
, lub 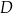 , lub
, lub 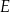 , lub
, lub 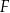 .
. 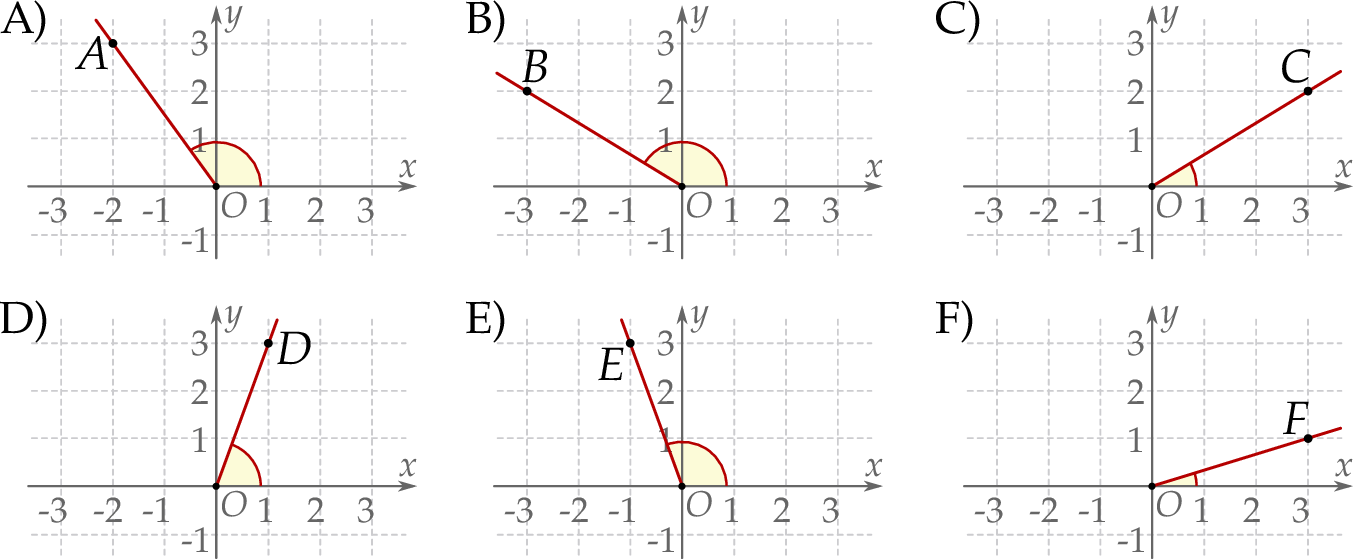
 , spełniający warunek
, spełniający warunek 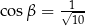 , jest zaznaczony na rysunku …
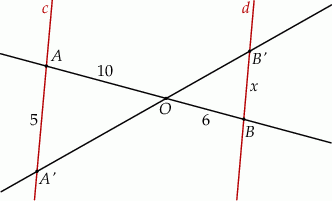
, jest zaznaczony na rysunku … 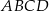 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 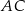 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 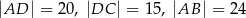 . Wtedy
. Wtedy 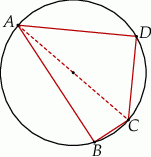
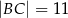
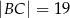
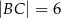
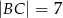
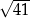
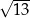
 i
i 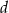 są równoległe. Jaką długość ma odcinek
są równoległe. Jaką długość ma odcinek  ?
? 
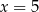
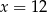
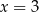
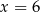
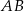 i
i 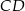 są równoległe. Odcinek
są równoległe. Odcinek 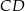 ma długość
ma długość 
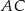 i
i 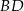 przecinają się w punkcie
przecinają się w punkcie 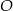 . Ponadto
. Ponadto 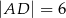 ,
, 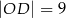 i
i 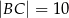 . Kąty
. Kąty 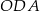 i
i 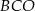 są proste (zobacz rysunek).
są proste (zobacz rysunek). 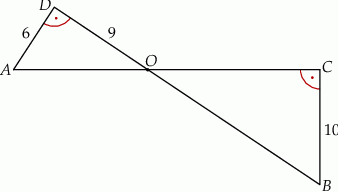
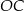 jest równa
jest równa 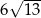
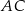 i
i 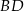 przecinają się w punkcie
przecinają się w punkcie 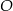 . Ponadto
. Ponadto 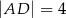 i
i 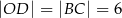 . Kąty
. Kąty 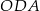 i
i 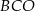 są proste (zobacz rysunek).
są proste (zobacz rysunek). 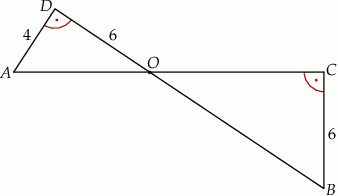
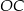 jest równa
jest równa 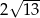
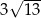
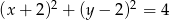 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu 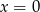
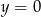
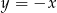
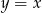
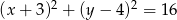 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu 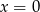
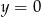
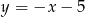
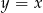
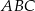 , w którym
, w którym 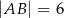 ,
, 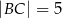 ,
, 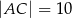 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 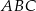 jest równy
jest równy 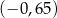 .
.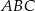 jest rozwartokątny.
jest rozwartokątny. 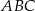 , w którym
, w którym 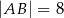 ,
, 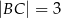 ,
, 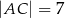 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 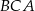 jest równy
jest równy 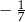 .
.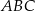 jest ostrokątny.
jest ostrokątny. 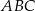 leżą na okręgu i środek
leżą na okręgu i środek 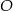 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 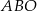 ma miarę
ma miarę 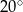 , to kąt
, to kąt 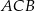 ma miarę
ma miarę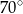
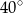
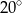
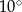
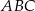 leżą na okręgu i środek
leżą na okręgu i środek  okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt  ma miarę
ma miarę 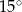 , to kąt
, to kąt 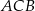 ma miarę
ma miarę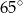
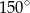
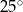
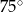
 opisano okrąg o środku
opisano okrąg o środku 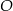 . Miara kąta
. Miara kąta 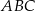 jest równa
jest równa 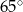 . Miara kąta
. Miara kąta 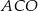 jest równa
jest równa 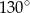
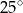
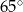
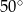
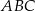 leżą na okręgu i środek
leżą na okręgu i środek 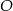 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 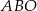 ma miarę
ma miarę 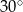 , to kąt
, to kąt 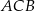 ma miarę
ma miarę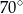
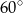
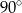
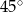
 poprowadzono cięciwę
poprowadzono cięciwę 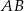 , która utworzyła z promieniem
, która utworzyła z promieniem 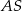 kąt o mierze
kąt o mierze 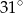 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 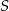 od cięciwy
od cięciwy 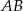 jest liczbą z przedziału
jest liczbą z przedziału 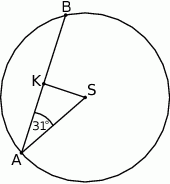
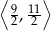
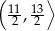
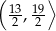
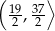
 poprowadzono cięciwę
poprowadzono cięciwę  , która utworzyła z promieniem
, która utworzyła z promieniem 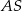 kąt o mierze
kąt o mierze 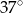 (zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy
(zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy 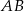 jest liczbą z przedziału
jest liczbą z przedziału 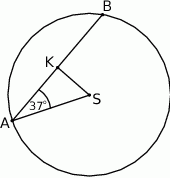
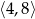
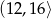
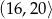
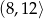
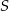 poprowadzono cięciwę
poprowadzono cięciwę 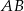 , która utworzyła z promieniem
, która utworzyła z promieniem 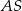 kąt o mierze
kąt o mierze 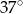 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 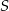 od cięciwy
od cięciwy 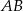 jest liczbą z przedziału
jest liczbą z przedziału 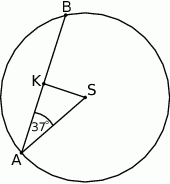
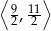
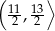
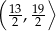
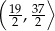
 mają długości
mają długości 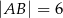 i
i 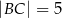 . Sinus największego kąta tego trójkąta jest równy
. Sinus największego kąta tego trójkąta jest równy  . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 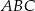 jest mniejsze od 10.
jest mniejsze od 10. 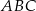 trójkąta
trójkąta 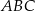 jest równy
jest równy 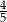 .
.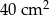
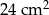
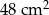
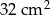
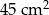
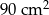
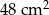
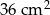
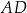 i
i 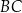 okręgu o środku
okręgu o środku 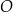 przecinają się w punkcie
przecinają się w punkcie 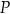 tak, że
tak, że 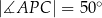 (zobacz rysunek).
(zobacz rysunek). 
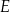 jest punktem wspólnym prostych
jest punktem wspólnym prostych 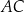 i
i 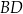 , to miara kąta
, to miara kąta 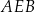 jest równa
jest równa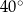
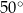
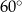
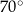
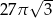
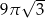
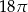
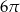
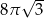
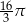
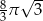
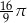
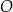 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 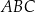 oraz
oraz 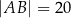 ,
, 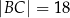 . Prosta
. Prosta 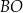 przecina bok
przecina bok 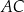 trójkąta
trójkąta 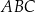 w punkcie
w punkcie 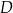 (zobacz rysunek).
(zobacz rysunek). 
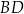 i
i 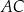 są prostopadłe.
są prostopadłe. 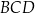 i
i 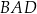 jest równy 0,9.
jest równy 0,9.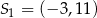 oraz okrąg o środku
oraz okrąg o środku 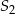 i promieniu 6 są styczne wewnętrznie w punkcie
i promieniu 6 są styczne wewnętrznie w punkcie 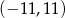 . Wtedy
. Wtedy 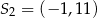
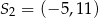
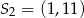
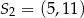
 i
i  leżą na okręgu o środku
leżą na okręgu o środku 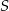 . Cięciwa
. Cięciwa 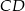 przecina średnicę
przecina średnicę 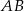 tego okręgu w punkcie
tego okręgu w punkcie 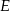 tak, że
tak, że 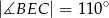 . Kąt środkowy
. Kąt środkowy 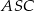 ma miarę
ma miarę 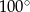 (zobacz rysunek).
(zobacz rysunek). 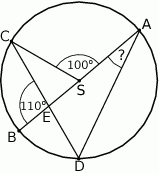
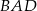 ma miarę
ma miarę 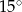
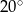
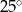
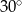
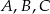 i
i  leżą na okręgu o środku
leżą na okręgu o środku 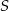 . Cięciwa
. Cięciwa 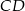 przecina średnicę
przecina średnicę 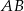 tego okręgu w punkcie
tego okręgu w punkcie  tak, że
tak, że 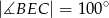 . Kąt środkowy
. Kąt środkowy 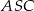 ma miarę
ma miarę 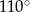 (zobacz rysunek).
(zobacz rysunek). 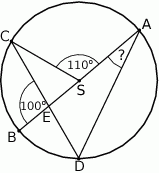
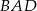 ma miarę
ma miarę 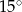
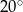
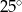
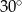
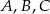 i
i 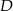 leżą na okręgu o środku
leżą na okręgu o środku 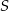 . Cięciwa
. Cięciwa 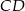 przecina średnicę
przecina średnicę 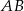 tego okręgu w punkcie
tego okręgu w punkcie 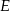 tak, że
tak, że 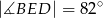 . Kąt środkowy
. Kąt środkowy 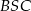 ma miarę
ma miarę 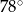 (zobacz rysunek).
(zobacz rysunek). 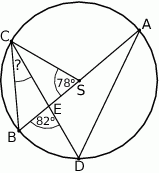
 ma miarę
ma miarę 
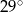
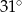
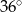
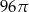
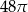
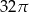
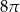
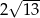 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa 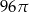
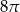
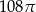
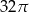
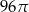
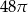
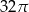
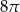
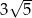 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa 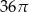
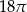
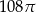
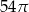
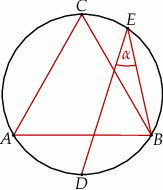
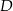 i
i 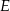 leżą na okręgu opisanym na trójkącie równobocznym
leżą na okręgu opisanym na trójkącie równobocznym 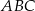 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 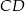 jest średnicą tego okręgu. Kąt wpisany
jest średnicą tego okręgu. Kąt wpisany 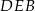 ma miarę
ma miarę  .
. 
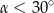
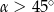
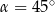
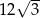 . Bok tego sześciokąta ma długość
. Bok tego sześciokąta ma długość 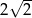
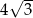
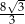 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy 
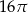 (mniejszy okrąg jest styczny do boków kwadratu
(mniejszy okrąg jest styczny do boków kwadratu 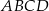 , a do większego okręgu należą punkty
, a do większego okręgu należą punkty 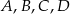 ). Zatem długość boku kwadratu
). Zatem długość boku kwadratu 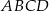 jest równa:
jest równa: 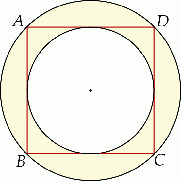
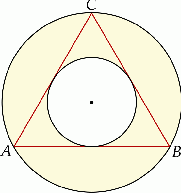
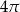 (mniejszy okrąg jest wpisany w trójkąt
(mniejszy okrąg jest wpisany w trójkąt 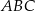 , a wierzchołki
, a wierzchołki 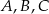 leżą na większym okręgu). Zatem długość boku trójkąta równobocznego
leżą na większym okręgu). Zatem długość boku trójkąta równobocznego 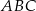 jest równa:
jest równa: