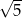W trójkącie 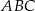 bok
bok 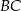 ma długość 13, a wysokość
ma długość 13, a wysokość 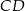 tego trójkąta dzieli bok
tego trójkąta dzieli bok 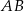 na odcinki o długościach
na odcinki o długościach 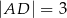 i
i 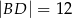 (zobacz rysunek obok).
(zobacz rysunek obok).
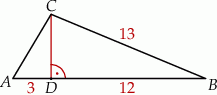
Długość boku 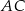 jest równa
jest równa
A) 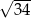 B)
B) 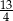 C)
C) 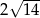 D)
D) 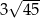
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 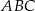 bok
bok 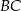 ma długość 13, a wysokość
ma długość 13, a wysokość 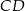 tego trójkąta dzieli bok
tego trójkąta dzieli bok 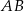 na odcinki o długościach
na odcinki o długościach 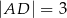 i
i 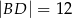 (zobacz rysunek obok).
(zobacz rysunek obok).

Długość boku 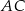 jest równa
jest równa
A) 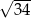 B)
B) 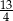 C)
C) 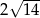 D)
D) 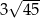
W trójkącie 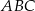 bok
bok 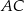 ma długość 10, a wysokość
ma długość 10, a wysokość 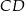 tego trójkąta dzieli bok
tego trójkąta dzieli bok 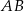 na odcinki o długościach
na odcinki o długościach 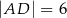 i
i 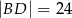 (zobacz rysunek obok).
(zobacz rysunek obok).
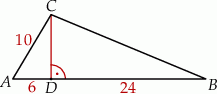
Długość boku 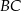 jest równa
jest równa
A) 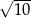 B)
B) 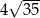 C)
C) 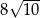 D)
D) 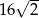
W trapezie równoramiennym podstawy mają długości 10 i 16, a kąt rozwarty ma miarę 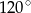 . Obwód trapezu jest równy
. Obwód trapezu jest równy
A) 38 B) 26 C) 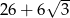 D) 32
D) 32
W trapezie równoramiennym podstawy mają długości 8 i 10, a kąt rozwarty ma miarę 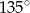 . Obwód trapezu jest równy
. Obwód trapezu jest równy
A) 24 B) 22 C) 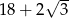 D)
D) 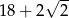
W trapezie równoramiennym podstawy mają długości 5 i 8, a kąt rozwarty ma miarę 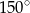 . Obwód trapezu jest równy
. Obwód trapezu jest równy
A) 19 B) 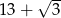 C)
C) 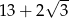 D) 16
D) 16
Dane są punkty o współrzędnych 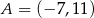 oraz
oraz 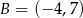 . Średnica okręgu wpisanego w sześciokąt foremny o boku
. Średnica okręgu wpisanego w sześciokąt foremny o boku 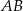 jest równa
jest równa
A) 10 B) 5 C) 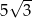 D)
D) 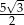
W trójkącie równoramiennym 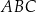 długość podstawy
długość podstawy 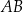 jest równa 4, a długość ramienia
jest równa 4, a długość ramienia 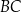 jest równa 6. Dwusieczna kąta
jest równa 6. Dwusieczna kąta 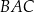 przecina bok
przecina bok 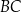 w punkcie
w punkcie 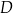 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 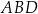 jest prostokątny. jest prostokątny. | P | F |
Odcinek 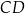 jest krótszy od odcinka jest krótszy od odcinka 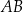 . . | P | F |
Symetralne boków trójkąta równobocznego przecinają się w punkcie odległym od wierzchołka o 5 cm. Wysokość tego trójkąta ma długość
A) 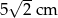 B)
B) 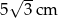 C)
C) 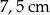 D)
D) 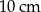
Symetralne boków trójkąta równobocznego przecinają się w punkcie odległym od boku trójkąta o 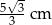 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 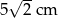 B)
B) 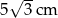 C)
C) 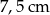 D)
D) 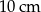
Pole powierzchni bocznej stożka wynosi 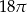 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 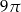 B)
B) 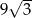 C)
C) 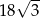 D)
D) 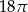
Pole powierzchni bocznej stożka wynosi 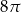 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 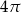 B)
B) 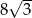 C)
C) 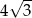 D)
D) 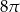
Prosta przechodząca przez środek 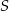 kwadratu
kwadratu 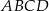 przecina proste zawierające jego boki
przecina proste zawierające jego boki 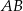 i
i 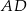 odpowiednio w punktach
odpowiednio w punktach 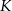 i
i 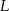 (zobacz rysunek).
(zobacz rysunek).
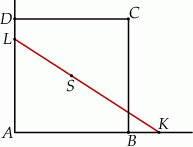
Jeżeli bok kwadratu ma długość 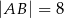 i
i 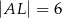 , to pole trójkąta
, to pole trójkąta 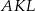 jest równe
jest równe
A) 32 B) 36 C) 40 D) 52
Graniastosłup ma 15 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 10 B) 5 C) 15 D) 30
Graniastosłup ma 18 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 18 B) 6 C) 12 D) 24
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wtedy liczba wszystkich jego wierzchołków jest równa
A) 6 B) 8 C) 12 D) 16
Liczba wszystkich krawędzi graniastosłupa jest równa 42. Liczba wszystkich wierzchołków tego graniastosłupa jest równa
A) 14 B) 28 C) 15 D) 42
Pole trójkąta przedstawionego na rysunku jest równe
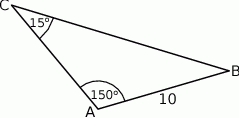
A) 50 B) 25 C) 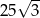 D)
D) 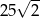
Pole powierzchni całkowitej czworościanu foremnego jest równe 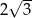 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 12 B) 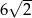 C)
C) 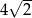 D)
D) 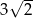
Pole powierzchni całkowitej czworościanu foremnego jest równe 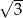 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 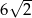 B) 3 C) 4 D) 6
B) 3 C) 4 D) 6
Na rysunku przedstawiono siatkę czworościanu foremnego.
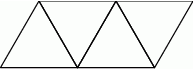
Jeżeli pole powierzchni całkowitej tego czworościanu jest równe 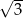 , to suma długości jego krawędzi jest równa
, to suma długości jego krawędzi jest równa
A) 9 B) 6 C) 4 D) 3
Prosta prostopadła do prostej 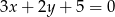 ma równanie:
ma równanie:
A) 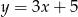 B)
B) 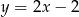 C)
C) 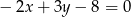 D)
D) 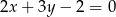
Prostą prostopadłą do prostej o równaniu 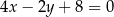 jest prosta o równaniu
jest prosta o równaniu
A) 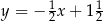 B)
B) 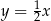 C)
C) 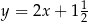 D)
D) 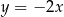
Prostą prostopadłą do prostej o równaniu 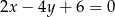 jest prosta o równaniu
jest prosta o równaniu
A) 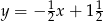 B)
B) 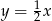 C)
C) 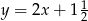 D)
D) 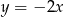
Prosta prostopadła do prostej 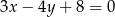 ma równanie:
ma równanie:
A) 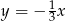 B)
B) 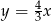 C)
C) 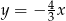 D)
D) 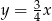
Dana jest prosta 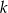 o równaniu
o równaniu 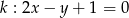 . Spośród podanych prostych wybierz prostą prostopadłą do
. Spośród podanych prostych wybierz prostą prostopadłą do 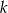 .
.
A) 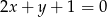 B)
B) 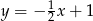 C)
C) 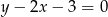 D)
D) 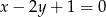
Wskaż równanie prostej prostopadłej do prostej o równaniu 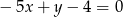 .
.
A) 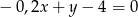 B)
B) 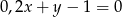 C)
C) 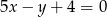 D)
D) 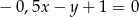
Prosta 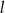 ma równanie
ma równanie 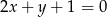 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do  .
.
A) 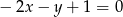 B)
B) 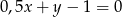 C)
C) 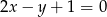 D)
D) 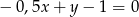
Prosta prostopadła do prostej 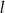 o równaniu
o równaniu 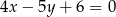 ma wzór
ma wzór
A) 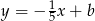 B)
B) 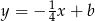 C)
C) 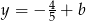 D)
D) 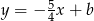
Dany jest czworokąt 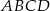 wpisany w okrąg o środku
wpisany w okrąg o środku 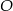 . Wówczas, jeśli
. Wówczas, jeśli 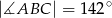 , to miara kąta
, to miara kąta 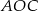 jest równa
jest równa
A) 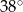 B)
B) 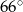 C)
C) 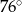 D)
D) 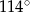
Dany jest czworokąt 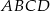 wpisany w okrąg o środku
wpisany w okrąg o środku 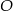 . Wówczas, jeśli
. Wówczas, jeśli 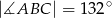 , to miara kąta
, to miara kąta 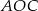 jest równa
jest równa
A) 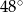 B)
B) 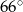 C)
C) 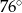 D)
D) 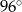
Dany jest czworokąt 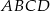 wpisany w okrąg o środku
wpisany w okrąg o środku 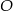 . Wówczas, jeśli
. Wówczas, jeśli 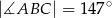 , to miara kąta
, to miara kąta 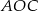 jest równa
jest równa
A) 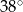 B)
B) 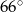 C)
C) 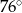 D)
D) 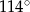
Prosta 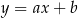 ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
A) przecina tylko oś 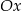 B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi 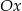 D) jest równoległa do osi
D) jest równoległa do osi 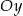
Punkty wspólne prostej 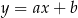 z osiami układu współrzędnych pokrywają się. Zatem prosta ta
z osiami układu współrzędnych pokrywają się. Zatem prosta ta
A) przecina tylko oś 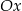 B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi 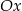 D) jest równoległa do osi
D) jest równoległa do osi 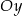
Jeżeli  jest kątem ostrym pod jakim przecinają się proste
jest kątem ostrym pod jakim przecinają się proste 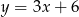 i
i 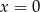 , to
, to
A) 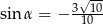 B)
B) 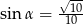 C)
C) 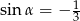 D)
D) 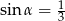
Dany jest prostopadłościan o wymiarach 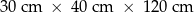 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 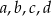 , o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
, o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
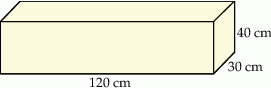
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 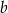 .
.
C) tylko od odcinków 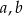 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dany jest prostopadłościan o wymiarach 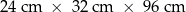 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 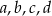 , o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
, o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
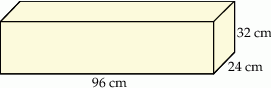
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 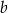 .
.
C) tylko od odcinków 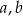 i
i  .
.
D) od wszystkich czterech danych odcinków.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa jest równy
A) 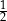 B)
B) 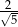 C)
C) 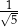 D)
D) 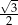
Okrąg o równaniu 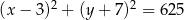 jest styczny do okręgu o środku
jest styczny do okręgu o środku 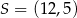 i promieniu
i promieniu  . Wynika stąd, że
. Wynika stąd, że
A) 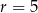 B)
B) 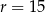 C)
C) 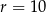 D)
D) 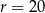
Okrąg o równaniu 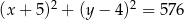 jest styczny do okręgu o środku
jest styczny do okręgu o środku 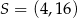 i promieniu
i promieniu  . Wynika stąd, że
. Wynika stąd, że
A) 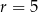 B)
B) 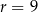 C)
C) 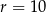 D)
D) 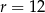
Pole powierzchni całkowitej prostopadłościanu o wymiarach 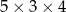 jest równe
jest równe
A) 94 B) 60 C) 47 D) 20
Pole powierzchni całkowitej prostopadłościanu o wymiarach 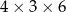 jest równe
jest równe
A) 94 B) 54 C) 108 D) 72
Promień okręgu opisanego na prostokącie o bokach: 6 cm i 8 cm jest równy:
A) 7 cm B) 6,5 cm C) 5 cm D) 10 cm
Dany jest sześcian 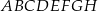 . Przekątne
. Przekątne 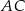 i
i 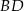 ściany
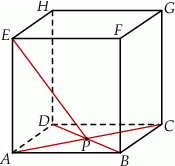
ściany 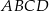 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 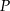 (zobacz rysunek).
(zobacz rysunek).
Tangens kąta, jaki odcinek 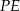 tworzy z płaszczyzną
tworzy z płaszczyzną 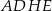 , jest równy
, jest równy
A) 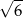 B)
B) 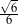 C)
C) 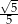 D)
D)