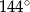W trójkącie równoramiennym 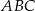 o podstawie
o podstawie 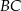 dane są:
dane są: 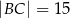 oraz
oraz 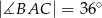 . Odcinek
. Odcinek 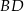 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 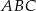 (zobacz rysunek).
(zobacz rysunek).
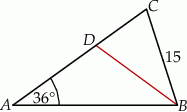
Wówczas długość odcinka 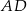 jest równa
jest równa
A) 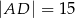 B)
B) 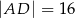 C)
C) 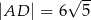 D)
D) 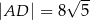
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie równoramiennym 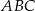 o podstawie
o podstawie 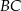 dane są:
dane są: 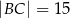 oraz
oraz 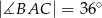 . Odcinek
. Odcinek 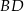 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 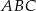 (zobacz rysunek).
(zobacz rysunek).

Wówczas długość odcinka 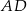 jest równa
jest równa
A) 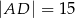 B)
B) 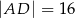 C)
C) 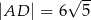 D)
D) 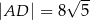
Okrąg o równaniu 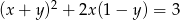 ma promień równy
ma promień równy
A) 3 B) 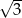 C) 4 D) 2
C) 4 D) 2
Okrąg o równaniu 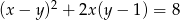 ma promień równy
ma promień równy
A) 9 B) 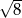 C) 3 D) 8
C) 3 D) 8
Do okręgu należą punkty 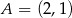 ,
, 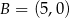 ,
, 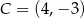 . Jest to okrąg o środku
. Jest to okrąg o środku 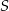 i promieniu
i promieniu  :
:
A) 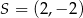 ,
, 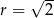 B)
B) 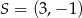 ,
, 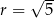
C) 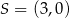 ,
, 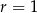 D)
D) 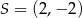 ,
, 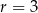
Przekątna 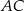 trapezu równoramiennego
trapezu równoramiennego 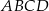 jest prostopadła do ramienia
jest prostopadła do ramienia 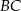 oraz tworzy z ramieniem
oraz tworzy z ramieniem 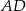 kąt ostry
kąt ostry  . Wysokość trapezu opuszczona z wierzchołka
. Wysokość trapezu opuszczona z wierzchołka 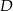 i ramię
i ramię 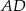 przecinają się pod kątem ostrym
przecinają się pod kątem ostrym 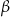 o mierze
o mierze 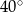 (zobacz rysunek).
(zobacz rysunek).
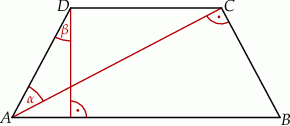
Wtedy kąt  ma miarę
ma miarę
A) 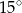 B)
B) 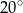 C)
C) 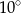 D)
D) 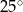
Która z podanych prostych jest styczna do okręgu 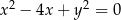 ?
?
A) 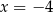 B)
B) 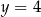 C)
C) 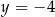 D)
D) 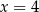
Która z podanych prostych jest styczna do okręgu 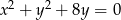 ?
?
A) 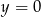 B)
B) 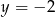 C)
C) 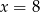 D)
D) 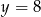
Oś 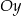 kartezjańskiego układu współrzędnych jest osią symetrii czworokąta
kartezjańskiego układu współrzędnych jest osią symetrii czworokąta 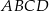 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek jednej z przekątnych czworokąta 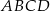 musi leżeć na osi musi leżeć na osi 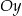 . . | P | F |
Czworokąt 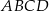 musi być trapezem. musi być trapezem. | P | F |
Średnicą okręgu jest odcinek 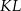 , gdzie
, gdzie 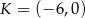 i
i 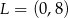 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 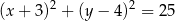 B)
B) 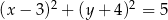
C) 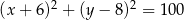 D)
D) 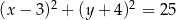
Okrąg o równaniu 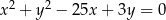 przecina oś
przecina oś 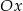 w punktach
w punktach
A) 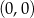 i
i 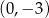 B)
B) 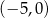 i
i 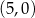
C) 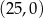 i
i 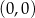 D)
D) 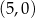 i
i 
Okrąg o równaniu 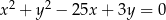 przecina oś
przecina oś 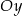 w punktach
w punktach
A) 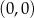 i
i 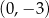 B)
B) 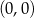 i
i 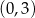
C) 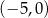 i
i 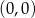 D)
D) 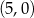 i
i 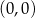
Jeśli długość jednego boku prostokąta zwiększymy o 20%, a długość drugiego boku prostokąta zmniejszymy o 5%, to pole prostokąta zwiększy się o:
A) 12% B) 14% C) 15% D) 16%
Jeśli długość jednego boku prostokąta zmniejszymy o 20%, a długość drugiego boku prostokąta zwiększymy o 5%, to pole prostokąta zmniejszy się o:
A) 12% B) 14% C) 15% D) 16%
Odcinek o końcach 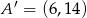 i
i 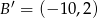 jest obrazem odcinka
jest obrazem odcinka 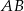 w jednokładności o skali
w jednokładności o skali 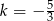 . Długość odcinka
. Długość odcinka 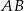 jest równa
jest równa
A) 12 B) 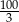 C) 16 D)
C) 16 D) 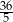
Odcinek o końcach 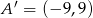 i
i 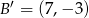 jest obrazem odcinka
jest obrazem odcinka 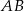 w jednokładności o skali
w jednokładności o skali 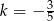 . Długość odcinka
. Długość odcinka 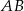 jest równa
jest równa
A) 12 B) 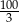 C) 16 D)
C) 16 D) 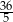
Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 15. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 9 B) 7 C) 6 D) 5
Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 25. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 9 B) 5 C) 6 D) 15
W kartezjańskim układzie współrzędnych 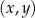 dany jest okrąg
dany jest okrąg 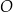 o równaniu
o równaniu
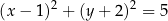
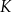 jest obrazem okręgu
jest obrazem okręgu 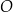 w symetrii środkowej względem początku układu współrzędnych. Okrąg
w symetrii środkowej względem początku układu współrzędnych. Okrąg 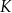 jest określony równaniem
jest określony równaniem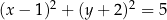 B)
B) 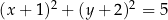
C) 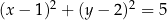 D)
D) 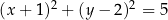
Wskaż równanie okręgu o środku 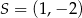 i promieniu
i promieniu 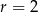 .
.
A) 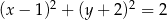 B)
B) 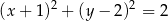
C) 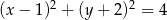 D)
D) 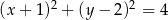
W kartezjańskim układzie współrzędnych 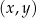 dany jest okrąg
dany jest okrąg 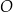 o środku
o środku 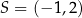 i promieniu 3. Okrąg
i promieniu 3. Okrąg 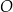 jest określony równaniem
jest określony równaniem
A) 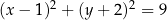 B)
B) 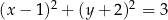
C) 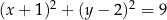 D)
D) 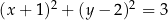
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 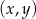 , dany jest okrąg o środku
, dany jest okrąg o środku 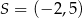 i promieniu
i promieniu 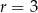 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 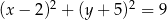 B)
B) 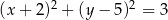
C) 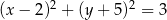 D)
D) 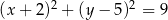
Okrąg ma środek 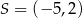 i promień
i promień 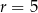 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 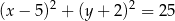 B)
B) 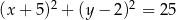
C) 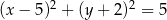 D)
D) 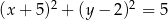
Wskaż równanie okręgu o środku w punkcie 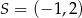 i promieniu
i promieniu 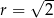 .
.
A) 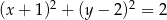 B)
B) 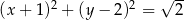
C) 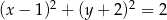 D)
D) 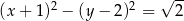
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 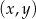 , dany jest okrąg o środku
, dany jest okrąg o środku 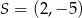 i promieniu
i promieniu 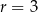 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 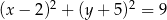 B)
B) 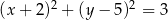
C) 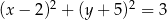 D)
D) 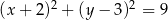
W kartezjańskim układzie współrzędnych 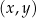 dany jest okrąg
dany jest okrąg 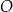 o środku
o środku 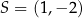 i promieniu 3. Okrąg
i promieniu 3. Okrąg 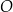 jest określony równaniem
jest określony równaniem
A) 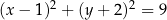 B)
B) 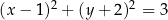
C) 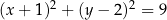 D)
D) 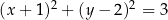
Pole trójkąta 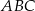 o wierzchołkach
o wierzchołkach 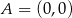 ,
, 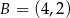 ,
, 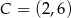 jest równe
jest równe
A) 5 B) 10 C) 15 D) 20
Pole trójkąta 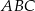 o wierzchołkach
o wierzchołkach 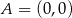 ,
, 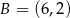 ,
, 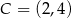 jest równe
jest równe
A) 10 B) 5 C) 20 D) 15
Nierówność 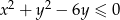 przedstawia koło o polu równym
przedstawia koło o polu równym
A) 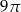 B)
B) 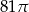 C)
C) 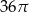 D)
D) 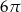
Nierówność 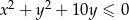 przedstawia koło o polu równym
przedstawia koło o polu równym
A) 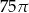 B)
B) 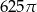 C)
C) 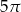 D)
D) 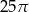
Nierówność 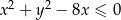 przedstawia koło o polu równym
przedstawia koło o polu równym
A) 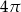 B)
B) 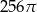 C)
C) 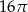 D)
D) 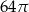
Okrąg, którego środkiem jest punkt 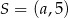 , jest styczny do osi
, jest styczny do osi 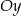 i do prostej o równaniu
i do prostej o równaniu 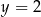 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 3 B) 5 C) 2 D) 4
Okrąg, którego środkiem jest punkt 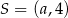 , jest styczny do osi
, jest styczny do osi 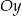 i do prostej o równaniu
i do prostej o równaniu 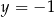 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 3 B) 5 C) 2 D) 4
Figura płaska 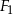 jest podobna do figury
jest podobna do figury 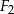 . Obwód figury
. Obwód figury 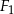 stanowi 40% obwodu
stanowi 40% obwodu 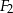 , zaś pole figury
, zaś pole figury 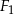 wynosi 8. Pole figury
wynosi 8. Pole figury 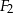 jest równe:
jest równe:
A) 50 B) 40 C) 25 D) 20
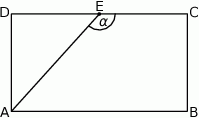
W prostokącie 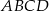 dane są
dane są 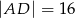 oraz
oraz 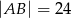 . Punkt
. Punkt 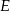 jest środkiem odcinka
jest środkiem odcinka 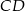 . Wówczas sinus kąta
. Wówczas sinus kąta 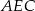 jest równy
jest równy
A)  B)
B)  C)
C) 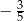 D)
D) 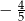
Z odcinków o długościach: 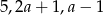 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 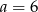 B)
B) 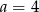 C)
C) 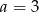 D)
D) 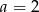
Z odcinków o długościach: 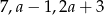 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 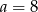 B)
B) 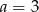 C)
C) 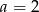 D)
D) 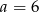
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 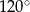 B)
B) 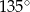 C)
C) 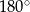 D)
D)